Khởi đầu là sự ngẫu nhiên

 

Hà Dương Tuấn

 

Abstract. Before Mankind appeared on the Earth, proliferating and cluttering the whole planet with man-made artefacts, random phenomena governed the incipient stage of every physical and biological being. This paper addresses random phenomena and their role within physics and biology. It comes into 3 parts. Firstly, it describes how random phenomena are dealt with mathematically. Secondly, it shows how probability mathematics and experimentation have finally clarified the well-known EPR paradox, a long − -standing controversy between Einstein and Bohr. Thirdly, the Darwinian explanatory scheme is discussed, together with key concepts such as randomness and emergence... The essay concludes by suggesting that the future of Mankind, from now on, will defeat any possible explanatory scheme.

1. Khởi đầu và khởi thuỷ

Ngẫu nhiên là một khái niệm khoa học để biểu diễn một lớp hiện tượng quan trọng có mặt khắp nơi và thường trực trong đời sống. Người có văn hoá ngày nay không thể thiếu một hiểu biết tối thiểu về ngẫu nhiên. Và, cũng như hai mặt của một đồng tiền, ngẫu nhiên không thể tách rời khỏi người anh em sinh đôi của nó là tính tất định. Ngẫu nhiên và tất định liên hệ với nhau thế nào, chúng có vai tṛ ǵ trong cơ học lượng tử (CHLT) và trong thuyết tiến hoá, hai lư thuyết nằm ở nền tảng của thế giới vật lư và thế giới sinh học[1]? Đó là chủ đề của tiểu luận này. Theo ḍng phát triển chúng ta sẽ gặp một khái niệm hiện đại quan trọng nữa, có liên hệ chặt chẽ với sự h́nh thành những thực thể phức tạp, đó là khái niệm hợp trội[2], cùng với người anh em sinh đôi của nó là khái niệm quy giản.

Tựa đề của tiểu luận này "khởi đầu là sự ngẫu nhiên" phải chăng có hậu ư muốn thay thế cho "khởi thuỷ là lời" của Thiên Chúa giáo, một tôn giáo lớn của nhân loại? Xin thú thật, hậu ư th́ có, nhưng để thay thế th́ không. V́ khởi đầu không phải là khởi thuỷ. Nói về khởi đầu dễ hơn, cụ thể hơn; mỗi khởi đầu có thể là của một sự vật, thực thể, khái niệm nhất định nào đó; trong khi khởi thuỷ th́ chỉ có một, cho cả vũ trụ. Khoa học không thể đoan chắc bất cứ điều ǵ về khởi thuỷ, v́ lẽ đơn giản là nó không thể đi ngược thời gian đến tận cùng. Vậy xin tôn trọng niềm tin của hàng tỷ người, và trở lại với những khởi đầu, với những ngẫu nhiên và tất định tác động lên những sự vật cụ thể trong thế giới vật lư và trong sinh giới.

2. Ngẫu nhiên và... ngẫu nhiên

Ta sẽ thấy, cái ngẫu nhiên trong vi mô và cái ngẫu nhiên trong kích thước con người là hoàn toàn khác nhau, không phải chỉ do kích thước, mà v́ một hiện tượng cơ bản của cơ học lượng tử khiến cho Einstein phải thốt ra "Thượng Đế không chơi tṛ súc sắc". Nhưng Einstein đă nhầm, Thượng Đế quả có chơi tṛ súc sắc, có điều rằng tṛ súc sắc của Thượng Đế (nếu muốn ta có thể thay thế "Thượng Đế" bằng "Tự Nhiên" viết hoa) trong CHLT khác hẳn những tṛ súc sắc khác.

2.1. Ngẫu nhiên đơn giản của đời thường

Khi ta ném một ḥn súc sắc trên mặt bàn, nó nhảy nhót, xoay chuyển, rồi khi nó đứng yên ta có một con số chọn giữa 1, 2, 3, 4, 5, 6, một cách ngẫu nhiên. Thật sự ngẫu nhiên, theo nghĩa kinh nghiệm cho thấy các con số xuất hiện với tần số rất gần nhau sau một thời gian quan sát dài, và theo nghĩa mọi người đánh cuộc đều tự ḿnh biết rằng không ai đoán được kết quả nên đă chọn một con số cầu âu như những người khác. Do đó nếu con súc sắc cân bằng, nếu không có gian lận, th́ những người đánh cược trên kết quả gieo súc sắc là thế này hay thế khác đều vui ḷng chấp nhận ḿnh đă thua hay được.

Nhưng thật ra chuyển động của con xúc sắc bị chi phối bởi những quy luật cơ học cổ điển, và nếu dùng một máy tính điện tử đủ mạnh gắn với máy quay phim để nhận dạng ḥn súc sắc khi nó ra khỏi bàn tay ném xuống bàn; th́ với vị trí, vận tốc và gia tốc chính xác, có thể tính ra kết quả trước khi con súc sắc dừng lại, với xác suất cao. Ở đây có một điều khiến cho rất khó có kết quả hoàn toàn chính xác, đó là hiện tượng "nhạy bén với điều kiện khởi đầu" do h́nh dạng của súc sắc và các chuyển động "sốc" của súc sắc trên bàn, khiến cho quỹ đạo bị phân tán rất nhanh theo thời gian. Điều kiện khởi đầu chỉ sai biệt chút xíu là kết quả tính toán sẽ khác hẳn. Nhưng điều này không ảnh hưởng đến hiện tượng cơ bản là kết quả gieo súc sắc bị chi phối bởi một biến số ẩn giấu[3], ảnh hưởng của trọng trường, mà khi xem xét một cách thống kê sau nhiều lần gieo người ta không cần biết đến. Người ta chỉ cần biết đến một hiện tượng thực nghiệm đơn giản hơn nhiều, đó là: xác suất xuất hiện của mỗi con số đều xấp xỉ 1/6; hiện tượng này xác nhận một lư luận cũng đơn giản: do tính đối xứng h́nh học của 6 mặt súc sắc và tính đồng nhất trong phân phối trọng lượng của nó, không có ǵ cho phép phân biệt mặt này với mặt khác.

2.2. Tiên đề hoá hiện tượng ngẫu nhiên

Tiên đề hoá hiện tượng ngẫu nhiên là một bước phát triển thiết yếu của toán học, được Kolmogorov thực hiện vào những năm 1920, tiếp nối công tŕnh của những tên tuổi lớn trong lịch sử toán học như Laplace, Poisson, Gauss, Lévy…, mở ra khả năng nghiên cứu những hiện tượng ngẫu nhiên phức tạp của tự nhiên và xă hội, khi tập hợp các hiện tượng cần nghiên cứu không chỉ là một tập hữu hạn hay đếm được. Lư thuyết xác suất ra đời và trở thành một lĩnh vực then chốt trong toán học cũng như vật lư học, sinh học hiện đại.

Cơ sở của các tiên đề Kolmogorov là một tập hợp A và một họ Φ các tập hợp con của nó – mà mỗi phần tử biểu diễn một hiện tượng ngẫu nhiên – và một hàm số P xác định trên Φ.

Khi A là hữu hạn hay đếm được th́ Φ sẽ gồm tất cả các tập hợp con của A, nếu không, Φ chỉ là một phần (một họ) các tập hợp con đó nhưng phải tuân theo các tiêu chí sau:

a/ A và Ø (tập hợp rỗng) là phần tử của Φ ;

b/ Nếu a Î Φ th́ A\a (tập hợp bù của a) cũng có trong Φ ;

c/ Nếu (a_i) là một chuỗi phần tử của Φ th́ hợp của chúng (È a_i ) cũng ở trong Φ.

Như vậy, hợp và giao của bất kỳ một số hiện tượng nào, hữu hạn hay vô hạn đếm được, cũng sẽ là một hiện tượng.

C̣n hàm số P, biểu diễn xác suất của các hiện tượng, phải thoả măn những điều kiện sau:

• Với bất kỳ a Î Φ nào, 0 ≤ P(a) ≤ 1.

Chú giải: Xác suất tương ứng với bất cứ hiện tượng nào cũng không thể là số âm và không thể lớn hơn 1 (theo quy ước, P = 1 có nghĩa hiện tượng chắc chắn xảy ra, P = 0 có nghĩa chắc chắn nó không xảy ra, P = 1/2 có nghĩa hiện tượng xảy ra xấp xỉ một lần trên hai, nếu được lặp lại nhiều lần).

• Nếu các chỉ số i và j nằm trong tập hợp các số tự nhiên (0, 1, 2, ... đến vô tận), nếu a_i Î Φ và a_j Î Φ và a_i Ç a_j = Ø (điều kiện này là biểu diễn toán học của khái niệm hai hiện tượng độc lập) với bất kỳ cặp số (i,j) nào th́ P(a₀ È a₁ È a₂ È ... đến vô tận ) = P(a₀) + P(a₁) + P(a₂) + ... đến vô tận.

Chú giải: Xác suất tương ứng với hai hiện tượng độc lập là tổng của hai xác suất tương ứng, (thí dụ: xác suất gieo súc sắc với kết quả sẽ là một hoặc hai, bằng 1/3). Và điều kiện này được mở rộng đến vô tận để chuẩn bị cho những bài toán phức tạp hơn trong không gian liên tục.

• P(A) = 1

Chú giải: Không có hiện tượng nào nằm ngoài không gian xác suất (với thí dụ gieo súc sắc điều này chỉ có nghĩa: kết quả phải là một trong 6 mặt).

P sẽ được gọi là độ đo xác suất (mesure de probabilités) hay luật xác suất (loi de probabilités).

Bộ ba (A, Φ, P) với những tính chất trên đây sẽ được gọi là một không gian xác suất (espace des probabilités). Trong thực tế, thuật ngữ này cũng được dùng để chỉ tập hợp A (khi Φ và P không cần được nhắc lại).

Trong ví dụ của việc ném một con súc sắc, A sẽ là tập hợp {1, 2, 3, 4, 5, 6}, Φ là tập hợp của tất cả các tập hợp con của A, và (nếu con súc sắc là chính quy) hàm P sẽ là P({x}) = 1/6 với bất kỳ x Î A nào. Hiện tượng B = {1, 3} – súc sắc cho kết quả hoặc là 1, hoặc là 3 – sẽ có xác suất 1/6+1/6 = 1/3, v́ B = {1} È {3}.

Mở rộng ra, khi A là một tập hợp hữu hạn hay đếm được, một độ đo xác suất P có thể được xây dựng bằng cách cho một hàm số p trên A, với p(x) ³ 0, S p(x) = 1, và định nghĩa P(a) là tổng của những p(x), x Î a.

2.3. Ngẫu nhiên trong không gian liên tục

Khi tập A là liên tục, người ta có thể chứng minh là nếu p là một hàm xác định trên A, với p(x) ³ 0 nhưng p(x) > 0 với một số không đếm được x Î A, th́ hàm P xác định trên tất cả các tập hợp con a của A như cách trên (P(a) là tổng của những p(x), xÎ a) không thể thoả măn các điều kiện của một độ đo xác suất.

Người ta chỉ có thể xác định một hàm số p trên các phần tử của A, sao cho với một vùng thật nhỏ – tập hợp con – với độ đo là dx (quanh điểm x) của A th́ xác suất của hiện tượng dx tại điểm x – P(dx) – xấp xỉ bằng p(x)dx. Nghĩa là, khi nói về xác suất trong một vùng không gian liên tục th́ hiện tượng không phải là một điểm trong không gian đó, mà phải là một vùng không gian B nằm trong không gian toàn thể A. Tại sao dùng chữ hiện tượng? Để dễ nhớ ta có thể tưởng tượng A là một ṿng phấn vẽ trên bảng đen bằng gỗ, B là một vùng nhỏ của ṿng tṛn A, việc ném phi tiêu hàng trăm lần vào trong ṿng tṛn A thực hiện một quy luật xác suất, việc phi tiêu cắm đúng vào vùng B là hiện tượng B. Cũng như khi gieo súc sắc, mặt mang số 5 chẳng hạn, được đánh đồng với hiện tượng kết quả súc sắc cho ra số 5.

Thêm nữa A phải có đặc tính là đo được (mesurable)^([4]), nói một cách ngắn gọn dù không đủ chính xác, điều đó có nghĩa người ta có thể làm toán tích phân trên A. Khi đó hàm P trên một vùng B là tích phân của hàm p trên vùng đó. Chẳng hạn, nếu B=[a, b] là một khoảng trong R (tập hợp các số thực) th́:

P(B) = ̣B p(x)dx = ̣ab p(x)dx

Và khi hàm P thoả măn ba điều kiện đă liệt kê ở trên^([5]) th́ p(x) được gọi là hàm mật độ ngẫu nhiên (densité de probabilité) của quy luật xác suất P.

Điều có vẻ rắc rối này thực ra cũng tự nhiên, trong vật lư từ cổ điển đến hiện đại rất hiếm có chuyện một hiện tượng, ngẫu nhiên hay không, xảy ra tại một toạ độ x tuyệt đối chính xác. Khi người ta nói tại điểm x th́ bao giờ cũng có nghĩa là: ở trong một vùng dx nhỏ chung quanh x. Nhưng chẳng lẽ câu nào cũng phải nhắc lại một sự thật phổ quát như thế!

Và bây giờ, với những khái niệm về xác suất kể trên, chúng ta đến được một áp dụng trong việc t́m hiểu CHLT: Khi người ta nói: trong CHLT, xác suất xuất hiện của lượng tử tại một điểm x trong không - thời - gian là b́nh phương của biên độ sóng của phương tŕnh Schödinger tại điểm ấy, thực ra đó là một cách nói không chính xác, câu ấy có nghĩa chính xác như sau: xác suất xuất hiện của lượng tử trong một vùng nhỏ dx chung quanh x trong không-thời-gian là b́nh phương của biên độ sóng của phương tŕnh Schödinger tại điểm ấy, nhân với dx. Nói cách khác, b́nh phương của biên độ sóng của phương tŕnh Schödinger là một hàm mật độ ngẫu nhiên của việc lượng tử tương tác với thiết bị đo lường tại điểm ấy.

2.4. Các quy luật của ngẫu nhiên

Nhưng trước khi triển khai thêm về ngẫu nhiên lượng tử lại xin rẽ một đường ṿng nói về các quy luật ngẫu nhiên trước đă; v́ có nhiều quy luật ngẫu nhiên khác nhau; xác định một biến số là ngẫu nhiên chưa đủ, c̣n phải xem quy luật của nó nữa, điều này cũng có tầm quan trọng cơ bản trong việc t́m hiểu vật lư, sinh học, hay bất cứ dữ liệu xác suất thống kê nào.

Không những có nhiều quy luật ngẫu nhiên mà c̣n có vô tận các quy luật này, ngay trong thí dụ đơn giản của con súc sắc: hăy lấy một con súc sắc không đồng nhất về chất liệu, chẳng hạn như nặng hơn về phía mặt 1 một chút so với mặt 6, các mặt khác coi như cân xứng. Như thế con súc sắc có khuynh hướng cho thấy mặt 6 nhiều hơn một chút v́ cái nặng có khuynh hướng ở dưới, tức ta có một quy luật xác suất suy ra được từ [A, C, C, C, C, B] cho các mặt từ 1 đến 6, với B là một số dương nhỏ hơn 1 nào đó, B > A ; B > C; và A + B + 4C = 1.

Vậy có thể thấy là cũng có vô tận các quy luật xác suất cho những hiện tượng xảy ra trong một không gian xác suất liên tục. Tuy nhiên, trong điều kiện mà hiện tượng xác suất là hậu quả của những quy luật vật lư cơ bản, những quy luật này thường rất đơn giản và có tính vừa đồng đẳng trong không gian vừa bất biến trong thời gian, người ta thường chỉ phải xử lư một số nhỏ các loại quy luật xác suất khác nhau (dĩ nhiên, với điều kiện coi như không đáng kể những bất đối xứng hay bất đồng đẳng trên thực tế, sau khi đă giới hạn chúng ở mức có thể bỏ qua được bằng cách khảo sát một số đáng kể các trường hợp). Một vài thí dụ của các quy luật xác suất khác nhau là: các quy luật chuẩn (lois normales), sở dĩ có tên như vậy v́ người ta chứng minh đuợc chúng là những tiệm cận gần đúng của nhiều quy luật xác suất, trong một số điều kiện; quy luật của Poisson, mô tả sự xuất hiện ngẫu nhiên trong thời gian của các hiện tượng độc lập với nhau, với một khoảng thời gian trung b́nh biết trước giữa hai xuất hiện... thường các quy luật xác suất hợp thành những "gia đ́nh" quy luật có cùng dạng toán học và chỉ biến thiên theo một hai tham số nào đó. Một tham số quan trọng là giá trị trung b́nh, điều này dễ hiểu, tham số quan trong thứ hai là phương sai, phương sai càng nhỏ th́ các hiện tượng càng tập trung gần điểm trung b́nh.

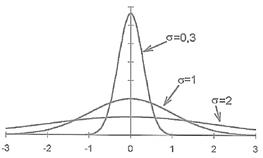
Thí dụ: hàm mật độ của các quy luật chuẩn,
với ba phương sai (variance) 0,3 ; 1 ; và 2.

3. Ngẫu nhiên và lượng tử

Tới đây ta đă tạm đủ hành trang để đề cập tới cuộc tranh căi suốt 20 năm giữa Einstein (1879 - 1955) và Bohr (1885 - 1962), không phải để hiểu rơ những chứng minh hay thí nghiệm, nhưng có lẽ đủ để hiểu về mặt khái niệm, họ đă nghĩ khác nhau ra sao, và hậu sinh của hai vị đă đóng góp vào cuộc thảo luận như thế nào. Cuộc tranh căi này có nội dung triết học sâu sắc, v́ nó liên hệ đến câu hỏi: thế giới vật chất là ǵ?

3.1. Bohr và nghịch lư đo lường

Theo Bohr, và trường phái Copenhagen, th́ CHLT là đầy đủ, theo nghĩa nó tiên đoán đầy đủ và chính xác các kết quả đo lường trong thực nghiệm - với điều kiện là chỉ nói đến các điều kiện và kết quả thực nghiệm mà thôi. Bất cứ cuộc thí nghiệm nào cũng sẽ được kết quả theo một xác suất đúng như phương tŕnh sóng của Schödinger tiên đoán. Phương tŕnh Schödinger là cơ bản nhất, không có ǵ ở "bên dưới" nó. Như thế có nghĩa là các kết quả xác suất của CHLT trong các đo lường thuộc về một loại ngẫu nhiên mới, cái ngẫu nhiên tuyệt đối không bị điều ǵ chi phối, khác về bản chất với việc con súc sắc bị chi phối bởi các quy luật cơ học cổ điển. Các tương tác lượng tử tuân theo những quy luật ngẫu nhiên có thể mô h́nh hoá được, chấm hết. Từ đó đến nay lập trường Copenhagen chưa hề bị phản nghiệm... Duy chỉ có một điều: nó chấp nhận tính bất đối xứng giữa thiết bị đo lường và lượng tử, mà hiển nhiên thiết bị đo lường cũng là vật chất được "làm bằng" các lượng tử. Nó không những không trả lời câu hỏi "thế giới vật chất là ǵ" mà c̣n thản nhiên chấp nhận những khác biệt bất khả liên thông giữa hai kích thước vi mô (lượng tử) và trung mô (máy đo lường). Điều này thật không làm trí tuệ con người thoả măn.

3.2. Einstein và nghịch lư EPR

Theo Einstein, và ông kiên định lập trường này cho tới cuối đời, th́ CHLT là không đầy đủ, theo nghĩa nó không chỉ ra được một "biến số ẩn giấu" trong các hiện tượng ngẫu nhiên của tương tác lượng tử (v́ theo ông các quy luật cơ bản nhất của thế giới khách quan phải là tất định, không thể có cái ngẫu nhiên tuyệt đối). Ông (E) cùng hai cộng sự là Podolski (P) và Rosen (R) đă đề ra một t́nh huống nghịch lư được gọi là nghịch lư EPR[6], nhằm chứng tỏ tính không đầy đủ đó[7]. Ba tác giả E.P&R. dựa trên ba khẳng định sau:

a) Những tiên đoán của CHLT là đúng;

b) Giữa hai vật chất không có ảnh hưởng nào có thể truyền nhanh hơn vận tốc ánh sáng (Thuyết tương đối là đúng);

c) Nếu ta có thể tiên đoán được một tính chất nào đó của một thực thể, mà không hề tác động lên nó, th́ tính chất ấy mang phẩm chất của hiện thực.

Diễn tả của người viết bài: nói cách khác, v́ không có ǵ tác động lên thực thể mà vẫn biết được thực thể có tính chất ấy, cho nên tính chất ấy phải là một thuộc tính hiện thực của thực thể, một biến số "nằm trong" thực thể, mặc dù biến số ấy có thể "ẩn giấu" và chỉ được biết đến trên thực nghiệm qua các kết quả xác suất[8].

Và E.P&R. đề ra một t́nh huống giả tưởng (t́nh huống EPR), một thí nghiệm tư duy mà theo họ có thể cho thấy cả ba tiền đề trên là đúng. Đề xuất này được công bố năm 1935, nhưng t́nh huống thí nghiệm tư duy quá phức tạp, không thể làm cho trở thành hiện thực với khả năng của công nghệ đương thời. Năm 1952 David Bohm cải biến t́nh huống EPR nguyên thuỷ thành một t́nh huống (hiện nay vẫn gọi là EPR) dễ xử lư hơn. T́nh huống này dựa trên sự liên hệ giữa hai lượng tử A và B trong một điều kiện thí nghiệm nhất định: khi đó nếu đo một thuộc tính của lượng tử gọi là spin, ta sẽ thấy spin của A và spin của B có tổng số bằng không. Đó là hiện tượng "vương vấn lượng tử" (intrication/entanglement quantique).

Vậy nếu đo spin(A) ta sẽ tiên đoán được spin(B) như E.P&R. mô tả trong điểm c) nói trên. Và điều này có thể được kiểm nghiệm rất sát nhau trong thời gian và đủ xa trong không gian để hai cuộc đo không có ảnh hưởng lên nhau như mô tả trong điểm b).

3.3. Phản bác của Bohr

Cả vấn đề là: spin(A) và spin(B) – hay một cái ǵ đó sẽ trở thành spin(A) và spin(B) – "có trước" và "nằm trong" A và B trước khi đo, như E.P.&R. nghĩ ; hay nói đến spin(A) và spin(B) trước khi đo chúng là vô nghĩa, như Bohr khẳng định? Với diễn tả Copenhagen th́ trước khi đo chỉ có phương tŕnh sóng Schödinger, và phương tŕnh này, trong trường hợp hai lượng tử "vương vấn" với nhau, th́ không phải hai phương tŕnh độc lập mà chỉ có một phương tŕnh thôi, cho một thực thể thôi[9], mặc dù thực thể đó, khi bị đo, th́ trở thành hai lượng tử độc lập ở cách xa nhau! Như vậy không thể nói là không tác động lên B khi đo A. Điểm c) của EPR là không được thoả măn, mặc dù hai điểm đo ở xa nhau và hai động tác đo rất gần nhau trong thời gian để không kịp truyền tin giữa A và B theo vận tốc ánh sáng.

T́nh huống giả tưởng này rút cục không làm thay đổi thái độ của cả hai bên, v́ bên nào cũng vẫn thấy lập trường của ḿnh không bị phủ nhận.

3.4. Bất đẳng thức Bell và thí nghiệm Aspect

Cho tới khi John Bell làm toán xác suất và t́m ra "bất đẳng thức Bell".

Đó là vào năm 1964, Bell chứng minh được định lư sau:

• Giả sử ta làm các đo lường (xin nhớ rằng trong CHLT mọi đo lường đều là những đo lường có tính xác suất) spin(A) và spin(B) theo điều kiện b) của EPR, th́:

• Có một đại lượng toán học S, tính toán được từ kết quả đo lường, mà, nếu phương tŕnh sóng Schödinger bị ảnh hưởng bởi một biến số ẩn giấu nào đó, với điều kiện là biến số đó tuân theo khẳng định b) nói trên của E.P.&R, tức chỉ có những ảnh hưởng cục bộ, nó sẽ ảnh hưởng đến kết quả đo lường để cho bất đẳng thức S ≤ 2.

Trong khi đó, người ta đă biết rằng nếu phương tŕnh sóng Schödinger mô tả sự ngẫu nhiên cơ bản nhất của tương tác lượng tử, th́ tính toán được là S = 2,70. Bất đẳng thức Bell do đó mở ra khả năng phân định đúng sai giữa Bohr và Einstein bằng thí nghiệm.

Đầu những năm 1970 có một số thí nghiệm nhằm chứng minh CHLT không tuân theo bất đẳng thức Bell, nhưng không đủ chính xác... Đến 1982, Alain Aspect và cộng sự công bố những kết quả của họ, cuộc thí nghiệm này không đo spin mà đo vectơ phân cực của các photon, hiện tượng tương đương về mặt lư thuyết. Họ đạt trị số S = 2,697, với sai số 0,015. Kết quả này được công nhận rộng răi, không ai c̣n nghi ngờ.

3.5. Tương tác lượng tử

Tóm lại, thực nghiệm đă cho thấy diễn tả Copenhagen (nói chính xác hơn, sự không diễn tả bản thể luận) là đúng. Nhưng, song song với quá tŕnh phát triển lư thuyết và thực nghiệm trong hơn nửa thế kỷ, lập trường "bất khả tri" cứng rắn như của Bohr cũng trở nên không c̣n cần thiết, v́ từ thời Einstein và Bohr tới nay CHLT đă đi tới một bước rất xa trong việc mô h́nh hoá nhất quán và có hiệu quả thế giới khách quan. Trong mô h́nh chuẩn, lư thuyết CHLT được đồng thuận hiện nay, tất cả là những trường lượng tử (tên mới của thực thể toán học được mở rộng từ phương tŕnh sóng Schödinger, do Dirac thực hiện để kết hợp được CHLT với thuyết tương đối hẹp), và mọi hiện tượng đều khởi đầu bằng tương tác giữa các trường lượng tử. Khởi đầu là sự ngẫu nhiên.

Có cần nói thêm là, tuy với CHLT người ta luôn luôn phải xét đến đầy đủ những điều kiện thí nghiệm, trong mô h́nh chuẩn không có một vai tṛ nào cho ảnh hưởng chủ quan của "người quan sát", như những hiểu lầm (xuất phát từ giai đoạn đầu của CHLT, khi ngay cả các nhà vật lư lớn nhất cũng thật sự bàng hoàng về những nghịch lư của nó) đến nay vẫn c̣n sống dai dẳng bên ngoài môi trường vật lư học.

Tương tác lượng tử là sự ngẫu nhiên tuyệt đối[10], một loại ngẫu nhiên khác các ngẫu nhiên của đời thường, không phải ngẫu nhiên v́ kết quả của các tác động lên hiện tượng − theo một quy luật ẩn giấu mà người ta không cần biết cụ thể − được phân bố một cách có thể mô h́nh hoá bằng một quy luật ngẫu nhiên nào đó, mà ngẫu nhiên v́ không có cái ǵ tác động lên hiện tượng cả, chỉ biết các tương tác lượng tử vẫn cứ xảy ra, theo một quy luật^([11]) ngẫu nhiên của phương tŕnh sóng Schödinger. Có quả mà không có nhân.

Và quan niệm rằng mọi tương tác trong thế giới khách quan phải có tính cục bộ là sai.

C̣n lại những phê phán về tính bất khả liên thông giữa kích cỡ lượng tử và kích cỡ đời thường; điều này cũng đă được giải quyết bằng lư thuyết "décohérence"; theo đó, t́nh trạng "vương vấn lượng tử" chỉ kéo dài trong một thời gian rất ngắn, và thực thể càng phức tạp th́ thời gian đó càng ngắn, ngắn tới mức trên thực tế không thể phân biệt. Sự chuyển tiếp giữa cái bất định, ngẫu nhiên, và không cục bộ, của kích cỡ lượng tử sang cái tất định, ổn định, và cục bộ, của các kích cỡ cao hơn, do đó là điều giải thích được. Và khi ta không nh́n th́ mặt trăng vẫn c̣n đó.

Tới đây đă quá dài về cái ngẫu nhiên trong kích cỡ vi mô. Xin tạm dừng để chuyển sang một câu hỏi khác, trở về với thuyết tiến hoá: có liên hệ ǵ giữa cái ngẫu nhiên tuyệt đối của tương tác lượng tử và cái ngẫu nhiên trong di truyền hay không?

4. Ngẫu nhiên và chọn lọc tự nhiên

Câu trả lời hiện nay là không có liên hệ trực tiếp. Các nghiên cứu sinh học với những thành công rất lớn trong thế kỷ vừa qua, bao gồm cả cuộc cách mạng về ADN, vẫn độc lập với hai cuộc cách mạng trong vật lư là thuyết tương đối và thuyết lượng tử. Tất cả nền sinh học hiện đại vẫn hoạt động trong một môi trường vật lư và hoá học cổ điển. Vậy khái niệm ngẫu nhiên trong sinh học là biểu hiện của những "biến số ngẫu nhiên ẩn giấu" của các quy luật vận động cơ bản hơn theo cơ học và hoá học cổ điển ở "tầng dưới" mà ta không thể chế ngự v́ quá phức tạp[12]. Nhưng! thế giới này chỉ là một, và, dưới dạng vật chất của nó, vũ trụ bị chi phối bởi những quy luật nhân quả do thuyết tương đối và thuyết lượng tử giải thích, do đó suy đến cùng th́ các quy luật sinh học bị ngẫu nhiên lượng tử chi phối một cách gián tiếp.

4.1. Quy giản và hợp trội

Nhiều khi ta không cần chế ngự những hiện tượng "ở tầng dưới" (theo phương pháp luận quy giản, réductionisme) để hiểu biết và sử dụng những hiện tượng ở tầng trên. Một thí dụ là quy luật Boyle - Mariotte, trong điều kiện nhiệt độ cố định th́ tích số của thể tích và áp suất của một khối lượng khí nhất định là hằng số: PV = P'V'. Định luật này khởi đầu là sự công nhận một hiện tượng thực nghiệm, trước khi người ta biết rằng vật chất là một tập hợp các nguyên tử hay phân tử. Nhưng ngày nay, nếu coi một khối lượng khí như một tập hợp các phân tử dao động và va chạm với nhau, ta có thể dùng toán xác suất, theo những ư tưởng của Boltzmann, để suy ra quy luật Boyle Mariotte cũng như những quy luật khác của thể khí. Cơ học thống kê do Boltzmann khai sinh đă quy giản hoá những quy luật hợp trội[13] về thể khí của thế kỷ 17 bằng cách đó, hay nói ngược lại nó đă giải thích bằng toán học được những hiện tượng hợp trội nói trên[14].

Khoa học chính xác về thế giới vô cơ cho đến nay nhằm xác định những hiện tượng vật chất, giải thích tại sao chúng xảy ra, biến chuyển, và triệt tiêu, bằng những quy luật nhân quả. Những định luật này ngày càng phổ quát và ngày càng đi sâu vào những thành phần nhỏ bé nhất của vật chất. Do đó, quy giản là một phương pháp luận khoa học thiết yếu, theo phương pháp ấy người ta đă giải thích được sự h́nh thành và bền vững của các nguyên tố hoá học bằng CHLT, giải thích được sự h́nh thành và bền vững của các phân tử hữu cơ bằng các định luật hoá học, nhưng các định luật hoá học cũng được giải thích bằng CHLT... Tuy các quy luật của CHLT là những quy luật xác suất, nhưng chính từ những quy luật xác suất đó mà người ta suy ra được tính ổn định của các chất hoá học và các định luật "tất định" của hoá học... trên thực tế phải coi các quy luật CHLT là những quy luật tất định khi chúng được sử dụng với một số nhỏ các xác suất hữu hạn với sai số không đáng kể, ngay trong những áp dụng cần độ chính xác cao nhất.

Quy giản - tất định là một sơ đồ lư giải[15] cho một lớp hiện tượng trong thế giới khách quan, sơ đồ này cũng có thể gọi là sơ đồ lư giải Descartes: phân chia một hiện tượng phức tạp thành nhiều bộ phận nhỏ đơn giản hơn và nghiên cứu những quy luật tất định cho từng bộ phận đó ; sau cùng tổng hợp lại bằng cách nghiên cứu những tác động hỗ tương giữa các thành phần, cũng theo những quy luật tất định. Vậy hai bộ phận chủ yếu của sơ đồ lư giải quy giản - tất định là phương pháp quy giản và các quy luật tất định (gồm cả các quy luật xác suất được "tất định hoá").

Hợp trội là một hiện tượng có thể thoát ra ngoài sơ đồ quy giản - tất định: với một hệ thống phức tạp th́ chỉ phân tích nó để t́m hiểu là không đầy đủ, v́ có những tính chất của hệ thống không thể t́m lại được bằng các quy luật vận động và tương tác tất định từ những thành phần. Do đó cần phân biệt hai tính chất hợp trội: loại hợp trội suy ra được từ những quy luật xác suất như tất cả những thí dụ nói trên, chúng vẫn nằm trong sơ đồ quy giản - tất định; và những hiện tượng hợp trội không suy ra được từ những vận động và tương tác của các thành phần, chỉ có thể tiên đoán được là nó có thể xảy ra (thường với một xác suất khá nhỏ) giữa hai tính chất hợp trội này có thể nhận thấy những khác biệt như sau:

Hợp trội tất định:	Chỉ có một số nhỏ hiện tượng "có thể" xảy ra, với các xác suất hữu hạn chính xác	rất nhiều vật thể thuộc rất ít loại vật thể khác nhau	rất ít kiểu tương tác và kết hợp	Thường áp dụng cho những hiện tượng vô cơ	Thí dụ: Các quy luật của thể khí, các quy luật hoá học...
Hợp trội không tất định:	Rất nhiều hiện tượng khác nhau có thể xảy ra với xác suất rất gần 0	nhiều vật thể thuộc nhiều loại khác nhau	nhiều kiểu tương tác và kết hợp	Thường áp dụng cho sinh học, xă hội học...	Thí dụ: Sự xuất hiện của các phân tử hữu cơ, sự sống...

Dĩ nhiên cả hai loại hợp trội đều bị chi phối bởi các quy luật tất định và các quy luật xác suất của thế giới khách quan. Vấn đề ở chỗ các quy luật này có phải là tất cả hay không? Có thể tin rằng suy đến cùng th́ không có một quy luật nào khác trong chi phối sự nảy sinh của các hiện tượng hợp trội không tất định, nhưng cũng có thể tin rằng có một điều ǵ khác cộng vào các quy luật tất định hay xác suất đă biết để chi phối sự nảy sinh của các hiện tượng hợp trội không tất định. Theo thiển ư, sự lựa chọn giữa hai thái độ là một vấn nạn siêu h́nh, v́ lập trường thứ hai không thể chứng minh được tính khoa học của ḿnh trừ phi tự phủ định: nếu "điều ǵ khác" đó được xác định một cách khoa học th́ đó sẽ là một quy luật mới của thế giới khách quan; và ngược lại, lập trường đầu không thể phủ định lập trường thứ hai một cách khoa học, v́ không thể chứng minh được bản thân ḿnh là đầy đủ, có những giả thuyết vĩnh viễn vượt khỏi khả năng tính toán.

Để đỡ nặng nề, kể từ đây khi trong bài này viết "hợp trội" trống không, đó là "hợp trội không tất định".

4.2. Sơ đồ lư giải Darwin

Lư giải đây là lư giải điều ǵ? Ở thời Darwin th́ ư tưởng về tiến hoá của các loài đă được nhiều người nói tới. Vấn đề là lư giải tại sao một loài sinh vật mới xuất hiện, và nó "tiến hoá" từ một loài sinh vật đă có. Từ trong một quần thể sinh vật sống trong một môi trường có thể biến đổi, có những cơ chế và tương tác nào đó làm cho một quần thể mới xuất hiện. Sự xuất hiện một loài sinh vật mới là việc có những cá thể được dị biến giống nhau và hợp thành một quần thể bền vững với thời gian. Sự bền vững này và những đặc tính mới có của quần thể là hoàn toàn đúng với ư nghĩa của từ "hợp trội" như đă mô tả.

Darwin là một nhà bác học vĩ đại của loài người (vào loại đếm được trên đầu ngón tay) có lẽ v́ ông là người đầu tiên đă sử dụng một sơ đồ lư giải khoa học khác với sơ đồ lư giải quy giản - tất định. Cũng như Lamarck trước ông nửa thế kỷ, ông tin vào sự tiến hoá của muôn loài; cũng như Lamarck ông quan sát vạn vật và t́m cách lư giải sự tiến hoá đó. Nhưng ông khác với Lamark ở hai khía cạnh lớn: một là công tŕnh quan sát vạn vật của ông vừa rộng vừa sâu hơn, hai là (có thể do đó) ông nhận ra những điều ḿnh không giải thích được nên không t́m cách giải thích. Từ đó ông gây ra một gián đoạn nhận thức so với Lamarck.

Theo Lamarck th́ sự biến dạng của sinh vật là do thích nghi với môi trường, v́ phải thích nghi nên biến dạng và sau đó sự biến dạng được giữ lại qua di truyền; thí dụ nổi tiếng là chuyện loài hươu cao cổ v́ phải ăn lá cây trên cao nên cổ cứ dài dần ra^([16]). Theo Darwin th́ sự biến dạng có trước, rồi quần thể nào v́ biến dạng mà t́nh cờ thích nghi được tốt th́ tồn tại − được chọn lọc một cách tự nhiên. Lamarck lư luận trên một "ư chí" nội tại của cá thể và Darwin lư luận trên các quần thể con của một quần thể rộng lớn hơn. Ông không giải thích tại sao có sự biến dạng, coi đó là một hiện tượng t́nh cờ của tự nhiên; ông cũng không giải thích tại sao sự biến dạng được giữ lại qua di truyền[17]. Một điểm nữa: ông giải thích sự biến mất của một số quần thể đă hiện hữu trong quá khứ qua việc các quần thể luôn mở rộng nhân số nhiều hơn tài nguyên môi trường có thể cung cấp^([18]), do đó có sự cạnh tranh để sinh tồn, và quần thể nào thích nghi tốt hơn sẽ tồn tại; đây là cạnh tranh trong sử dụng tài nguyên, không nhất thiết phải đấu tranh với nhau.

Vậy có thể tổng quát hoá sơ đồ lư giải Darwin cho những hiện tượng hợp trội trong sinh học như sau:

• Các loài sinh học sinh sản qua tiếp thu tài nguyên của môi trường chung quanh và sự sinh sản này sinh ra những dị biến ngẫu nhiên thành các quần thể phái sinh khác nhau
• Những quần thể mới nếu thích nghi tốt hơn với môi trường th́ bền vững hơn và sinh sản tốt hơn (bằng một cách nào đó những tính thích nghi tốt này được bảo tồn qua di truyền, và các quần thể này trở thành các loài mới). Những quần thể mới nếu không thích nghi tốt th́ sẽ bị đào thải, những loài cũ nếu không cạnh tranh nổi với loài mới sẽ bị mất nguồn nuôi sống và cũng sẽ bị đào thải.

Điểm sau này được gọi là sự chọn lọc tự nhiên. Nhưng nh́n lại chúng ta thấy nổi lên những vấn đề rất lớn chưa được giải quyết:

• Cơ chế của sự dị biến là như thế nào?
• Làm sao mà một dị biến nào đó lại ổn định?
• Cơ chế của di truyền là như thế nào?

Phải cần hơn một thế kỷ những vấn đề này mới được giải quyết tương đối ổn thoả, được sự đồng thuận trong khoa học, tuy rằng vẫn c̣n những khác biệt trong chi tiết. "Mô h́nh chuẩn" trong sinh học này được gọi là lư thuyết tân Darwin.

4.3. Lư thuyết tân Darwin

Sơ đồ lư giải Darwin, như chúng ta thấy, chỉ áp dụng cho những quần thể có khả năng tự sinh sản, v́ đó là giả định đầu tiên. Nói cách khác, nó có thể áp dụng cho những hiện tượng hợp trội trong sinh học kể từ khi các tế bào − thực thể đầu tiên có khả năng tự chia làm hai − xuất hiện. C̣n về hiện tượng hợp trội đầu tiên, là sự xuất hiện tế bào, th́ cho đến nay chỉ có những giả thuyết, kể cả giả thuyết các tế bào đến từ ngoài hành tinh. Từ khi có các tế bào, cách đây 3,8 tỷ năm (trái đất h́nh thành cách đây khoảng 4,5 tỷ năm) đă có không biết bao nhiêu hiện tượng hợp trội sinh học làm xuất hiện những sinh thể ngày càng phức tạp. Ở đây không liệt kê lịch tŕnh tiến hoá trong những tỷ năm đó, mà rất nhiều sách vở tài liệu đă nói đến, mà chỉ xin ghi lại một số điểm quan trọng có tính cách định tính:

• Sơ đồ tân Darwin thêm một điểm rất quan trọng vào sơ đồ Darwin, đó là giải thích sự biến dị qua cơ chế đột biến ngẫu nhiên trong di truyền. Sơ đồ này là một giả thuyết có từ những năm 1930 - 1940, và được minh chứng bởi việc khám phá cấu trúc ADN năm 1953 (Crick và Watson), khởi đầu cho những phát kiến sau đó của nhiều nhà sinh học về tác động của thông tin di truyền lên sự phát sinh h́nh thái, h́nh thành cả một bộ môn sinh học phân tử.
• Có hai cơ chế làm thay đổi thông tin di truyền, cơ chế "b́nh thường" là việc sinh sản có giới tính, theo đó các gien (genes) của người con là sự kết hợp bằng cách chọn lọc ngẫu nhiên, "cắt và dán" từ các gien của cha mẹ; và cơ chế "bất b́nh thường" là việc các chuỗi phân tử ADN bị chép sai trong quá tŕnh sinh sản. Cả hai hiện tượng đều là ngẫu nhiên.
• Tế bào thiết lập một thực thể có ranh giới "bên trong" và "bên ngoài", với một màng bao bọc. Màng tế bào cho phép phân biệt các tương tác giữa tế bào và môi trường chung quanh nó với các tương tác bên trong tế bào; các tương tác này có thể lại là phản ứng từ những tương tác trong/ngoài... các tế bào lại được kết hợp thành những bộ phận khác nhau, mỗi bộ phận lại có bên trong và bên ngoài... tiến tŕnh kết hợp này cứ thế tiếp tục thêm nhiều tầng phức tạp... cho đến h́nh thành "cái tôi" của một cá thể và cái "chúng ta" của một quần thể...
• Quá tŕnh phát sinh h́nh thái gồm những tác động qua lại hết sức phức tạp giữa sự bội biến của các tế bào, sự phân hoá từ những tế bào giống nhau thành những tế bào khác nhau, sự kết hợp chúng thành những bộ phận khác nhau của cơ thể, tất cả vừa dựa vào vừa bị khống chế bởi những quy luật tất định và những quy luật xác suất trong sự tương tác giữa các tế báo trong cơ thể với nhau và với môi trường bên ngoài[19].
• Người ta qua đó hiểu rơ hơn tính bền vững của một giống loài, v́ rất ít đột biến trong kiểu di truyền (génotype) có thể chuyển thành những đột biến khả dĩ ổn định của kiểu h́nh thái (phénotype); những quái thai thường chết yểu. Thêm nữa, do việc sinh sản có giới tính, sự hiện hữu của một số nhỏ sinh vật đột biến và ổn định cũng không đủ, phải có một quần thể ổn định, có số lượng tới hạn và đủ tương thích với nhau để sinh sản được, mới thành một loài mới, ổn định, có thể cạnh tranh sinh tồn[20]. Do đó mặc dù ngày nay người ta biết rằng việc sao chép ADN không có độ tin cậy cao, đột biến trong chuỗi ADN là chuyện cơm bữa; nhưng hiện tượng hợp trội để nảy sinh ra một loài mới (có thể thắng thế trong sinh tồn trong một thời gian dài hay ngắn) có một xác suất rất nhỏ. Các loài sinh vật là ổn định.
• Nhưng mặt khác, dù xác suất nói trên rất nhỏ th́ với thời gian tính bằng thế kỷ, thiên niên kỷ, hay ức triệu niên kỷ, cũng có những giống loài mới nảy sinh. Bí mật của hợp trội là thời gian.

Trở lại tiến tŕnh phát sinh h́nh thái. Nhà vật lư học lớn Schödinger trong [ES] nghĩ rằng tiến tŕnh này là một tiến tŕnh tất định^([21]), nói cách khác, thông tin di truyền có thể coi như một loại chương tŕnh được thực hiện song song bởi các tế bào, khiến cho các tế bào tương tác với nhau và với môi trường theo một sơ đồ lư giải quy giản - tất định, để cuối cùng h́nh thành sinh vật. Sau khám phá ADN và những cơ chế các chuỗi ADN điều khiển sự sinh trưởng, cả ngành sinh học phân tử cũng nghĩ và nghiên cứu theo hướng ấy. Nhưng những phát hiện gần đây[22] cho thấy tiến tŕnh phát sinh h́nh thái có lẽ đi theo một sơ đồ nửa quy giản - tất định nửa Darwin. Không phải các chuỗi ADN trong các tế bào làm ǵ cũng chắc chắn và đúng hướng trong "nhiệm vụ" của ḿnh. Chúng cũng "thử và sai" để rồi có những tế bào bị loại và những tế bào khác được chọn lựa theo những ức chế của môi trường bên trong cơ thể, những ức chế này cũng không cần thiết phải tuyệt đối tất định. Kết quả của những tiến tŕnh loại này thường không độc nhất, không tiên đoán được, và không tối ưu. Nếu "chấp nhận được" trong một khuôn khổ ức chế nhất định, nó sẽ tồn tại ổn định và góp phần xác định h́nh thái.

4.4. Ngẫu nhiên và t́nh cờ trong chọn lọc tự nhiên

Cần nhấn mạnh, quan sát một hiện tượng t́nh cờ[23] đơn lẻ không thể cho biết ǵ về quy luật xác suất ảnh hưởng trên nó. Chỉ có thể kiểm nghiệm một quy luật xác suất khi người ta quan sát thật nhiều hiện tượng và làm thống kê các trường hợp xảy ra giống nhau hay khác nhau... đó chính là ư nghĩa của chữ xác suất. Do đó toán học xác suất chỉ sử dụng được trong điều kiện quan sát và thống kê được trên nhiều lần các hiện tượng xảy ra trong một hoàn cảnh nào đó, nói đến xác suất cho một hiện tượng duy nhất đă xảy ra thường chỉ có ư nghĩa định tính và tượng trưng. Thí dụ như nói: "xác suất để loài người xuất hiện trên trái đất là rất nhỏ". Cứ cho rằng từ "loài người" tượng trưng cho một sinh vật có ư thức tương tự như chúng ta, và "trái đất" tượng trưng cho một hành tinh có điều kiện cho sự sống; với tŕnh độ khoa học hiện nay chúng ta có lẽ có thể ước lượng được số hành tinh như thế trong vũ trụ, nhưng làm sao biết trong số đó có bao nhiêu hành tinh có "loài người" cư ngụ? Vậy rất nhỏ là bao nhiêu? Nhưng dù cho có lớn như rất gần 1, hay nhỏ đến một phần tỷ tỷ tỷ đi nữa, th́ chúng ta cũng đă hiện hữu bây giờ và ở đây, như một người đă trúng số độc đắc, không thể biết tại sao. Có thể v́ nghĩ rằng xác suất đó rất nhỏ, nên lại nghĩ rằng phải có một quyền lực siêu nhiên nào đó sáng tạo ra chúng ta và cả vũ trụ này; xin cứ ngạc nhiên và hân hoan để làm những bài thơ hay trên niềm tin ấy; nhưng điều đó không có cơ sở khoa học[24].

Vậy xin phân biệt hai khái niệm: một hiện tượng phải có thể xuất hiện hay không xuất hiện nhiều lần trong một khung cảnh nhất định th́ mới nói được là hiện tượng ngẫu nhiên. Một hiện tượng độc nhất không biết nguyên nhân là một hiện tượng t́nh cờ. Nhưng xin để ư là "hiện tượng" c̣n tuỳ thuộc cách nh́n và định nghĩa. Những ǵ xảy ra tại cùng một nơi và cùng một lúc, tuỳ quan điểm có thể gọi là một hiện tượng ngẫu nhiên hay một chuyện t́nh cờ. Thí dụ: việc bạn tôi bị đụng xe ngày ấy tháng ấy tại nơi ấy là một chuyện t́nh cờ, v́ đó là việc độc nhất đă xảy ra cho bạn tôi, khái niệm xác suất không đặt ra ở đây. Nhưng chính cũng tai nạn xe hơi đó vào ngày ấy tháng ấy tại nơi ấy, là một hiện tượng ngẫu nhiên nằm trong xác suất thống kê cần thiết cho cảnh sát giao thông và cho các hăng bảo hiểm... Hiện tượng có một thiên thạch rơi xuống trái đất trong năm tới là một ngẫu nhiên mà các nhà thiên văn có thể cho biết xác suất. Nhưng việc một thiên thạch khổng lồ đă rơi xuống trái đất cách đây 65 triệu năm và làm đảo lộn con đường tiến hoá của các loài trên trái đất là một chuyện t́nh cờ, mà nếu không có nó không chắc đă có chúng ta hôm nay[25].

Hiện tượng t́nh cờ đó dĩ nhiên không phải độc nhất, nếu chúng ta nh́n vào sự sống trên trái đất hàng ngày, hiện nay, cũng thấy biết bao nhiêu chuyện t́nh cờ lớn hay nhỏ. V́ vậy mà, nếu lịch sử 3 tỷ năm của sự sống được diễn lại trong một khung cảnh thiên văn giống hệt từng ngày, th́ có thể đoan chắc rằng mọi giống loài tương đối phức tạp trên trái đất sẽ đều không như ngày nay.

Giả sử có một trí tuệ siêu phàm quan sát trái đất cách đây vài triệu năm thôi, trí tuệ đó cũng không thể tiên đoán được sẽ có một loài người như chúng ta. Sơ đồ lư giải Darwin có thể giải thích thoả đáng rất nhiều hiện tượng hợp trội, nhưng nó không thể làm điều bất khả. Nó chỉ giải thích được mà không tiên đoán được[26].

5. Để kết luận: Ngẫu nhiên, Tất định và Tự do

Tiểu luận này đă tŕnh bày v́ sao mà khởi đầu của mọi việc trong thế giới vật lư và trong thế giới sinh học đều do ngẫu nhiên (và cả t́nh cờ). Nhưng nếu bạn đọc câu này thấy chối tai th́ bạn hoàn toàn có lư. V́ cần phải nói thêm: ...trước khi có loài người. Con người là sản phẩm của quá tŕnh tiến hoá, một biện chứng phức tạp giữa ngẫu nhiên và tất định. Con người cũng mang theo nó hiện tượng hợp trội sinh học cao nhất và phức tạp nhất: nó trở thành sinh vật có ư thức, ư thức về thế giới khách quan, và ư thức về chính ḿnh. Với ư thức về chính ḿnh, con người đă chinh phục được Tự do hành động. Và, cộng với ư thức về thế giới khách quan, con người đă chinh phục được các quy luật của tự nhiên, làm tăng cao nguồn tài nguyên nuôi sống ḿnh, và lan tràn khắp trái đất.

Rồi đến ngày nay, chung quanh chúng ta đầy rẫy những sự vật mà điểm khởi đầu không hề là ngẫu nhiên: thành phố, căn nhà, cây cầu, bàn ghế, cái máy tính tôi đang dùng, ngọn đèn đang chiếu sáng... tất cả đều nhân tạo và đều là sản phẩm của ư thức con người.

Phải chăng sự tiến hoá của loài người từ nay sẽ không thể được lư giải theo sơ đồ Darwin nữa? Hay nói cho cùng, nó tự do có nghĩa tương lai của nó sẽ không thể được lư giải theo bất cứ sơ đồ nào?

Nhưng tự do đi đôi với hiểu biết và trách nhiệm. Loài người đang sống trong một môi trường bị đe doạ nặng nề bởi ư chí con người trong quá khứ và hiện tại, nhưng cũng chỉ có ư thức và ư chí con người, với đầy đủ hiểu biết và trách nhiệm, mới ngăn lại được sự xuống cấp của môi trường và cứu văn đời sống của các thế hệ con người tương lai.

Tác giả là chuyên gia công nghệ thông tin, Paris.

Tài liệu tham khảo:

[AM] Alexandre Meinesz, Comment la vie a commencé; coll. Pour la science, nxb Belin 2009.

[BE] Bernard d'Espagnat, A la recherche du réel; nxb Gauthier Villars 1979.

[BVNS] Bùi Văn Nam Sơn, "Tiến hoá như một sơ đồ lư giải", dẫn nhập cho bản dịch Nguồn gốc các loài của Charles Darwin, dịch giả Trần Bá Tín; nxb Tri Thức, 2009.

[EK] Etienne Klein, Petit voyage dans le monde des quanta; coll. Champs, nxb Flammarion 2004.

[ES] Erwin Schödinger, What is life?; nxb McMillan 1946. Bản dịch tiếng Pháp: Qu'est ce que la vie; nxb Seuil 1947.

[GCT] Gilles Cohen Tannoudji, Les constantes universelles; coll. Pluriek, nxb Hachette, 1998.

[FJ] François Jacob, Le jeu des possibles; coll. Livres de poche, nxb Fayard 1986, 7e édition 2007.

[JM] Jacques Monod, Le hasard et la nécessité; coll. points sciences, nxb Seuil 1970, 4e édition 1973.

[JJK - 1] Le blog d'Automates Intelligents: Entretien avec le biologiste Jean - Jacques Kupiec, 18.05.2009;

http://automatesintelligent.blog.lemonde.fr/2009/05/25/entretien - avec - le - biologiste - jean - jacques - kupiec/

[JJK - 2] Jean - Jacques Kupiec, Une approche Darwinienne de l'ontogenèse, 07.09.2009;

http://www.admiroutes.asso.fr/larevue/2009/99/ontophylogenese.htm

[JLB] Jean Louis Basdevant, 12 leçons de mécanique quantique; nxb Vuibert 2007.