Nam Dao giới thiệu:

Đẩy đến giới hạn, sự t́m hiểu vật giới của nhà khoa học và nhân giới của nhà văn có một thành tố chung. Đó là ḷng say mê. Và chính từ say mê họ sở đắc một bản chất chung: họ đều là những nghệ sĩ trong cuộc truy lùng những huyền diệu của bản giao hưởng giữa con người nhỏ nhoi hữu hạn với một vũ trụ vô cùng và bí ẩn. Cám ơn nhà khoa học Phạm Xuân Yêm đă chia sẻ với bạn đọc qua một bài viết khái quát nhưng rơ ràng về một lư thuyết vật lư quan trọng không mấy ai ‘’ngoại đạo’’ mà nắm được.

 

Phạm Xuân Yêm

Lược giải về thuyết tương đối

Nguồn : Talawas 9/2008

 

 

1. Ư tưởng sung sướng nhất trong đời tôi

Một chiều Chủ nhật cuối tháng Năm năm 1905 đẹp trời nắng ấm, Albert Einstein và anh bạn thân cùng sở làm Michele Angelo Besso dạo chơi trên đồi Gurten, xa xa dưới chân là thành phố Bern cổ kính hiền hoà, họ bàn luận trao đổi về bí hiểm ether ^[1] , rồi ngay tối hôm đó ông suy nghĩ tính toán và dần dần h́nh thành thuyết tương đối hẹp để vài tuần sau gửi đăng trên tạp chí uy tín thời đó Annalen der Physik. Trong ṿng hai năm, công tŕnh này gây được nhiều tiếng vang tán đồng trong giới hàn lâm và nghiên cứu (đặc biệt bởi Max Planck, người khai phá ra thuyết lượng tử mà dấu ấn ngày càng in đậm trong khoa học và công nghệ hiện đại), mặc dầu c̣n một số người nghi ngại v́ khái niệm cách mạng của thời gian không phổ quát mà co dăn. Nhà vật lư thực nghiệm tiếng tăm Johannes Stark ^[2] mời ông viết một bài tổng hợp về lư thuyết mới mẻ đó và b́nh luận về những hệ quả cùng triển vọng. Công việc đ̣i hỏi nhiều thời gian v́ ông vẫn phải tiếp tục tám giờ mỗi ngày, sáu ngày mỗi tuần làm việc tại Pḥng Đăng kư Bằng Sáng chế của thành phố Bern để nuôi tiểu gia đ́nh gồm hai vợ chồng và con trai Hans vừa tṛn ba tuổi. Nhưng hoàn tất bài tổng hợp đó cũng là phương cách để Einstein hy vọng t́m được một chức vụ giảng dạy và nghiên cứu ở đại học mà ông hằng ước mơ sau khi tốt nghiệp trường Bách khoa Kỹ thuật ở Zürich (ETH). Chỉ lúc rảnh rang trong giờ cạo giấy ông mới có đôi phút suy tư về vật lư. Rồi một ngày tháng Mười Một năm 1907, đang ngồi trong Pḥng Đăng kư, Einstein chợt nẩy ra một ư tưởng mà ông coi như măn nguyện nhất trong đời: một người rớt từ trên cao xuống không cảm thấy sức nặng của ḿnh. Theo ông kể, ư tưởng giản dị có vậy thôi, nhưng nó gây một ấn tượng mạnh khiến tôi vô cùng sửng sốt và dần dà đưa đẩy tôi khám phá ra một lư thuyết mới về hiện tượng vạn vật hấp dẫn. Để hiểu cái mới lạ ra sao, có lẽ không ǵ hơn là trở về thời điểm của cơ học cổ điển, khi Galileo Galilei (1564-1642) phát hiện ra tính chất phổ quát của vật chất rơi trong không trung bởi sức hút (hấp dẫn hay trọng lực) của trái đất, theo đó nếu vắng một sức cản nào của môi trường, không khí chẳng hạn, th́ mọi vật bất kể khối lượng lớn nhỏ ra sao, ở chung một chỗ trên cao sẽ rơi xuống hệt như nhau với cùng một gia tốc ^[3] . Chúng ta chưa quên h́nh ảnh mấy phi hành gia đầu tiên lên cung Hằng năm 1969 thả cái búa tạ cùng mấy sợi lông tơ để thấy chúng quả thực rơi xuống mặt trăng với cùng một gia tốc v́ ở đấy vắng không khí cản trở. Thí nghiệm này chỉ tượng trưng thôi chứ chẳng gây chút ngạc nhiên nào v́ lâu lắm rồi chính Isaac Newton (1643-1727), vài chục năm sau phát kiến của Galilei, đă chứng nghiệm tính phổ quát nói trên khi quan sát các chu kỳ dao động giống hệt nhau của mấy chiếc quả lắc đồng hồ nặng nhẹ khác nhau. Lực hấp dẫn, không như các lực cơ bản khác (lực của điện từ hay của các hạt nhân nguyên tử), mang đặc tính độc đáo là nó áp đặt một gia tốc duy nhất lên mọi vật thể đặt ở cùng một chỗ, bất kỳ khối lượng lớn nhỏ của vật đó.

Ngoài ra c̣n thêm một khía cạnh nữa là phương tŕnh căn bản của cơ học F = m γ bảo cho ta khối lượng m mang một đặc trưng là nó diễn tả tính trây ỳ hay quán tính của vật thể. Thực thế, bất kỳ một lực F nào (trọng lực, điện từ lực, lực hạt nhân, lực cơ bắp hay máy móc) khi áp đặt lên một vật A mang khối lượng m, vật đó sẽ chuyển động với gia tốc γ. Cũng một lực F ấy khi tác động lên một vật B khác mang khối lượng ba lần lớn hơn A th́ dĩ nhiên gia tốc của B so với A giảm đi ba lần, nó chuyển động chậm hơn A hay có quán tính lớn gấp ba lần A. Vậy khối lượng biểu lộ khả năng quán tính của vật thể chống lại sự di động. Kết hợp hai điều trên, trọng lượng ^[4] của một vật (lực mà vật ấy bị hút bởi trọng trường tạo nên bởi vạn vật trong vũ trụ) lại tỉ lệ thuận với tính trây ỳ của vật đó và tính phổ quát của Galilei được chứng minh khi ta dùng phương tŕnh cơ bản ^[5] của động lực học ^[6] .

Mối liên hệ sâu sắc giữa trọng lực, gia tốc và quán tính được Newton miêu tả - bằng ngôn ngữ toán học ngắn gọn và chính xác - trong định luật vạn vật hấp dẫn. Chủ yếu Newton, tuy không t́m được nguyên nhân tại sao có sự liên hệ như vậy, nhưng đă nhận ra là khối lượng của một vật A mang ba đặc trưng: (i) quán tính của A, (ii) A phải phản ứng ra sao khi trọng lực (tạo ra bởi một vật B khác ở ngoài) tác động lên nó, và (iii) chính vật A cũng tự nó sinh ra một trọng trường để lôi hút mọi vật khác ở xung quanh ^[7] và dĩ nhiên lên vật B. Trong ṿng hơn hai thế kỷ sau Newton, nhiều nhà khoa học, mặc dầu làm việc trong hệ h́nh (paradigm) của cơ học cổ điển, hầu như đă quên mất chuyện quan trọng này, chẳng c̣n mấy ai đào sâu t́m hiểu thêm ba vai tṛ tiên nghiệm rất biệt lập của khối lượng.


2. Và Einstein xắn tay mở khoá

Mối liên hệ giữa quán tính, gia tốc và trọng lực mà trực giác Einstein linh cảm thấy trong một buổi trưa tháng Mười Một năm 1907 phải gói ghém một tín hiệu nào đó và ông bắt đầu suy tư. Lao tâm khổ tứ, gian nan lặn lội trong sai lầm rồi tỉnh ngộ, khi vui lúc nản trong tám năm trường ^[8] để cuối cùng ngày 25 tháng Mười Một năm 1915 bừng sáng, ông rẽ mây chỉ lối cho nhân loại khai thác một kho tàng tri thức vô ngần sâu sắc, không những của vật lư mà cũng của vũ trụ quan và triết học nói chung. Ông mường tượng, trước hết ta sẽ quan sát được ǵ trong một cái thang máy đứt dây và rơi tự do trong không trung bởi tác động của trọng trường quả đất. Theo tính chất phổ quát của Galilei, tất cả mọi vật ở trong thang, kể cả chính nó đều rơi như nhau với cùng một gia tốc g, nên so với sàn thang th́ chúng hoặc đứng yên hoặc lướt đi đều đặn với vận tốc cố định. Ngày nay các phi hành gia lơ lửng trong những hỏa tiễn thám hiểm vũ trụ là h́nh ảnh quen thuộc của hiện tượng vô trọng lực. Bất kỳ mỗi điểm trong thang máy rơi đều có thể coi như một hệ qui chiếu quán tính ^[9] , trong đó trọng lực như bị xóa đi, phản ánh ư tưởng sung suớng nhất trong đời Einstein. Thêm bước nữa, ông mường tượng một nơi xa lánh tất cả mọi thiên hà tinh tú, một không gian ở đó vắng mặt trọng trường. Trong cái không gian vô trọng lực ấy, có một hộp mà ta đẩy mạnh lên cao với một gia tốc nào đó, ta thấy mọi vật ở trong hộp bị đẩy rơi ngược chiều xuống thấp với cùng một gia tốc, giống như hộp bị hút xuống bởi một trọng lực, điều quá quen thuộc trên xe hơi khi ta bất chợt nhấn mạnh phanh, mọi người như bị kéo về phía trước. Vậy th́ vận chuyển có gia tốc nào khác ǵ tác động của trọng trường, có một mối liên hệ mật thiết giữa gia tốc và sức hút của trọng lực. Những tác dụng của một trọng trường thực có thể như bị xóa bỏ trong một hệ qui chiếu rơi tự do (gia tốc ≠ 0), hoặc khi ta khảo sát vận chuyển có gia tốc, một trọng trường ảo như được tạo ra. Để hiểu lư do tại sao Einstein lại chú tâm đến gia tốc khi đang viết bài tổng hợp về thuyết tương đối hẹp (trong đó chỉ có sự di chuyển đều đặn, gia tốc = 0), mời bạn đọc trở về với nguyên lư tương đối mà Galilei tóm tắt trong một câu ngắn gọn "di chuyển đều đặn cũng như không’’, hàm ư rằng trong hai hệ quy chiếu, một cái đứng yên (tọa độ x,y,z,t), một cái di động đều đặn với vận tốc v cố định (tọa độ x’,y’,z’,t’), các định luật miêu tả thiên nhiên đều giống hệt nhau ^[10] , hay f(x,y,z,t) = f(x’,y’,z’,t’) hàm số f tượng trưng cho một định luật vật lư nào đó ^[11] . Khi nguyên lư này áp dụng cho điện từ để diễn tả vận tốc ánh sáng c không thay đổi trong tất cả các hệ quy chiếu quán tính th́ hàm số f chính là f(x,y,z,t) ≡ (x² + y² + z²) - (ct)². Đó là điểm khởi đầu, từ đó Einstein, Lorentz và Poincaré mỗi người một vẻ đă xây dựng nên thuyết tương đối hẹp (hay thuyết tương đối đặc biệt, phụ chú 12). Có lẽ trong tiềm thức, Einstein tự đặt câu hỏi, các định luật sẽ thay đổi ra sao trong trường hợp các hệ quy chiếu di chuyển không đều đặn, và khi phân tích những điều vừa kể trên về thang máy rơi, ông nhận ra vai tṛ quyết định của trọng trường trong sự nới rộng phạm vi không gia tốc của thuyết tương đối hẹp sang phạm vi có gia tốc của thuyết tương đối rộng (hay thuyết tương đối tổng quát). Câu "di chuyển đều đặn cũng như không’’ của Galilei, qua ư tưởng sung sướng nhất trong đời của Einstein, nay biến thành "di chuyển không đều đặn chẳng khác ǵ tác động của trọng lực’’, đă mở đầu một kỷ nguyên mới cho vật lư, nới rộng thuyết tương đối đặc biệt sang thuyết tương đối tổng quát để thay thế thuyết vạn vật hấp dẫn của Newton, định luật cổ điển này chỉ là truờng hợp xấp xỉ gần đúng của thuyết tương đối rộng vô cùng chính xác. Hơn nữa c̣n thêm một nguyên nhân thúc đẩy Einstein mở rộng thuyết tương đối đặc biệt v́ ông nhận ra có một mâu thuẫn giữa thuyết này (theo đó vận tốc của mọi tín hiệu đều có hạn, kể cả ánh sáng) và luật cổ điển vạn vật hấp dẫn (theo đó trọng lực truyền đi với vận tốc vô hạn để vạn vật hút nhau tức th́). Vậy bằng cách nào đó sửa đổi luật hấp dẫn Newton sao cho ḥa đồng với thuyết tương đối hẹp sẽ tự động giải đáp được mâu thuẫn nói trên. Dùng nguyên lư tương đương giữa gia tốc và trọng lực như một tiền đề, ông suy diễn, dùng dụng cụ toán học để t́m một định luật mới về hấp dẫn, hơn nữa c̣n đề xuất những hệ quả và tiên đoán những hiện tượng kiểm soát đo lường được. Cách tiếp cận cách tân như vậy khởi đầu từ Galilei - trong đó suy luận, phê phán bằng lư tính và kiểm chứng bằng thực nghiệm đóng vai tṛ chủ đạo - là bài học sâu xa cho hậu thế và tiếp tục làm kim chỉ nam cho tiến tŕnh nghiên cứu sáng tạo của khoa học ngày nay.


3. Không-thời gian bốn chiều biến dạng từ phẳng sang cong

3a. Vài điều sơ đẳng về thuyết tương đối hẹp, một giai đoạn tối quan trọng cần thấu triệt để đi xa hơn nữa trong tiến tŕnh khám phá ra thuyết tương đối rộng. Einstein khởi đầu bằng chấp nhận nguyên lư tương đối áp dụng cho điện từ như một tiền đề - theo đó vận tốc ánh sáng bao giờ cũng cố định và bằng c, không thay đổi trong bất kỳ các hệ quy chiếu quán tính nào - mà Michelson và Morley đă chứng tỏ bằng thực nghiệm. Trong hai hệ quy chiếu, một đứng yên (toạ độ x,y,z,t), một di chuyển đều đặn với bất kỳ vận tốc v cố định (toạ độ x’,y’,z’,t’), vận tốc ánh sáng không thay đổi được diễn tả bằng ngôn ngữ toán học là b́nh phương khoảng cách s² của ánh sáng truyền đi trong hai hệ quy chiếu phải như nhau hay bất biến ^[12] : s² ≡ (x² + y² + z²) - (ct)² = (x’² + y’² + z’²) - (ct’)². Với thời gian phổ quát duy nhất của Newton (t = t’) th́ s² không sao bất biến được và đă làm đau đầu bao nhà khoa học. Điểm then chốt của thuyết tương đối hẹp là các vị Lorentz, Poincaré, Einstein mỗi người một cách đă phát kiến ra hệ số k = 1 ⁄ √(1− v² ⁄c²) ≥ 1 ch́a khoá mở đường vô cùng quan trọng cho cơ học tương đối tính ^[13] . Từ tiền đề nguyên lư tương đối và hệ số k, Einstein suy ra nhiều hệ quả kiểm chứng được bằng thực nghiệm, trước hết là phương tŕnh E = kmc² của thế kỷ, liên kết năng lượng E khổng lồ với khối lượng m nhỏ bé ^[14] , tuyệt vời và đại chúng. Thông điệp thứ hai, sâu sắc và kỳ lạ, là chẳng có một thời gian tuyệt đối và phổ quát trong một không gian biệt lập với thời gian. Có muôn ức thời gian (t’ và t dẫu khác nhau nhưng cả hai đều chỉ định thời gian trong hai hệ quy chiếu) nhanh chậm không đồng đều, thời gian của mỗi hệ quy chiếu tùy thuộc vào vận tốc chuyển động của hệ ấy. Mỗi thời-điểm phải gắn quyện với mỗi không-điểm trong một thực tại bốn chiều gọi là thế giới Minkowski để diễn tả một sự kiện. Khoảng cách thời gian của bạn khác của tôi, ở mỗi điểm không gian lại gắn liền một đồng hồ đo thời gian với nhịp điệu tích tắc khác nhau ^[15] . Sở dĩ bạn và tôi tưởng rằng chúng ta chia sẻ một thời gian phổ quát, chỉ v́ cộng nghiệp con người trong cái không gian quá nhỏ bé của trái đất so với vũ trụ, bạn và tôi đâu có xa nhau ǵ, vận tốc tương đối giữa chúng ta thấm ǵ so với vận tốc ánh sáng (v²⁄c² « 1, k ≈ 1). Hơn nữa không có mũi tên thời gian lạnh lùng trôi của trực giác mà cơ học cổ điển Newton thừa nhận, cũng không có khái niệm hiện tại, cái bây giờ chẳng thể xác định và giữ vai tṛ ưu tiên đặc thù nào hết v́ cái lúc nào phải đi với cái ở đâu. Hơn nữa, không gian và vật chất, cái vỏ chứa và cái bị chứa, lại như h́nh với bóng trong vũ trụ vô thuỷ vô chung co dăn (thuyết tương đối rộng, xem phần 4, 5). Đă không có hiện tại th́ nói chi đến quá khứ và tương lai, đó là nội dung triết học quá ư kinh ngạc của thuyết tương đối hẹp và rộng trong nhận thức về thời gian, nó không phải là mũi tên trôi một chiều từ quá khứ đến tương lai mà chỉ là một trong bốn thành phần của thực tại mang tên gọi không-thời gian chẳng cứng nhắc mà đàn hồi. Diễn tả hàm súc nhất về nhận thức này có lẽ nằm trong bức thư Einstein gửi cho con trai của Besso ^[16] khi nghe tin bạn mất. Bức thư viết:  "Vậy bạn đă trước tôi một chút, giă từ cái thế gian lạ lùng này. Nhưng cái đó chẳng nghĩa lư ǵ. Đối với chúng ta, những nhà vật lư có xác tín, sự chia cách quá khứ, hiện tại, tương lai chỉ là một ảo tưởng, dẫu nó dai dẳng đến thế nào’’.

Điều cơ bản cần nhấn mạnh là không gian và thời gian chẳng c̣n biệt lập nhưng mật thiết liên đới trong một thực thể bốn chiều không-thời gian mà Einstein sẽ khai thác sâu xa thêm trong lư thuyết tương đối rộng với sự thay đổi toạ độ quy chiếu phi quán tính (gia tốc ≠ 0).

3b. Chúng ta khởi đầu đi từ không gian ba chiều tuyệt đối của Newton để sang thế giới không-thời gian bốn chiều của Minkowski, cả hai đều phẳng theo nghĩa h́nh học Euclid. Nếu khoảng cách vi phân b́nh phương trong không gian ba chiều là |dX|² = dx² + dy² + dz² (quỹ tích là mặt cầu Ѕ2 trơn tru) th́ b́nh phương khoảng cách vi phân ds² trong không-thời gian bốn chiều là ds² = (dx² + dy² + dz²) - (cdt)² (quỹ tích biểu hiện bởi h́nh hyperboloïd Ѕ3 trơn tru). Đó cũng là định lư Pythagoras mở rộng trong bốn chiều với các hệ số ±1 thay v́ chỉ có +1 của |dX|². Khi mở rộng quy mô vận chuyển không gia tốc của thuyết tương đối hẹp (với h́nh học phẳng của không-thời gian bốn chiều Minkowski) sang quy mô vận chuyển có gia tốc của thuyết tương đối rộng, năm 1912 (vâng 5 năm sau cái ư tưởng sung sướng nhất trong đời, trải qua bao nhiêu gian lao), trực giác của Einstein cảm thấy cấu trúc h́nh học phẳng sẽ phải biến dạng sang h́nh học cong ^[17] v́ gia tốc c̣n hàm nghĩa sự quay, uốn lượn mà mặt phẳng hay h́nh cầu trơn tru giản dị không diễn tả được hết cái phức tạp, tế nhị của mọi quỹ đạo trong thiên nhiên. Để thống nhất các kư hiệu toán dùng trong h́nh học bốn chiều phẳng hay cong, thay v́ t, x, y, z, ta hăy dùng bốn tọa độ ct ≡ x⁰, x ≡ x¹, y ≡ x², z ≡ x³, và định nghĩa một tứ-vectơ xμ là vectơ có bốn thành phần x0, x1, x2, x3 (thay v́ vectơ quen thuộc x với ba thành phần x,y,z trong không gian ba chiều). Trong h́nh học phẳng Minkowski, b́nh phương khoảng cách ds² = (dx² + dy² + dz²) - (cdt)² giữa hai không-thời điểm xμ và (xμ +dxμ) sẽ viết dưới dạng ds² = ημν dxμ dxν, các chỉ số μ (hay ν) có giá trị 0, 1, 2, 3 và hệ số ημν là những con số thực như +1 hay −1 (thí dụ ηoo = −1, ηi i = +1, ηoi = ηio = ηij = 0 với i ≠ j, i hay j là 1,2,3). Ngoài ra trong kư hiệu ngắn gọn ημν dxμ dxν, ta theo quy ước ^[18] Riemann-Einstein làm tổng hợp các đóng góp của cả hai chỉ số μ,ν.

Làm sao mở rộng sang h́nh học cong những hệ số ημν quá đơn sơ của h́nh học phẳng Minkowski? Einstein nhớ lại những bài giảng (của thầy dạy toán C.F.Geiser khi ông là sinh viên ở ETH) về mặt cong hai chiều Ѕ2 mà nhà toán và vật lư học trứ danh Karl F. Gauss ^[19] đă từng phân tích cấu trúc lồi lơm của mặt quả bóng bầu dục, so sánh với mặt quả cầu trơn tru. Ngoài ra c̣n công tŕnh của nhà toán học Bernhard Riemann, môn đệ của Gauss, đă tổng quát hóa kết quả của thầy từ bề mặt bầu dục hai chiều sang trường hợp nhiều chiều. Để mở đầu, ta hăy xét trường hợp những bề mặt hai chiều và nhận thấy khoảng cách giữa hai điểm kế cận vi phân trên mặt quả cầu tṛn trơn tru chẳng khác chút nào khoảng cách giữa hai điểm kế cận vi phân trên mặt phẳng, nếu ta h́nh dung bao quanh hai điểm trên mặt cầu bằng trang giấy phẳng tiếp xúc sát với h́nh cầu, và hai trục tọa độ thẳng góc trên h́nh cầu sẽ là hai đường kinh tuyến và vĩ tuyến quen thuộc của trái đất lư tưởng phẳng phiu tṛn trĩnh. Mặt cầu (như mặt phẳng) sẽ bị bao trùm bởi một mạng lưới gồm muôn vàn h́nh vuông vi phân, ta chỉ cần hai toạ độ x, y như trên mặt phẳng để xác định khoảng cách dl giữa hai điểm vi phân trên mặt cầu, dl² = dx² + dy². Nếu mặt cầu (hay bóng bầu dục) lồi lơm, ta cũng chẳng cần một tọa độ thứ ba để đo chiều cao hay chiều sâu, nhưng mạng lưới h́nh vuông sẽ thành mạng lưới của các h́nh b́nh hành bao bọc mặt cầu lồi lơm này. Định lư Pythagoras của h́nh b́nh hành (chữ nhật không vuông góc) cho ta khoảng cách dl giữa hai điểm vi phân của mặt hai chiều Ѕ2 lồi lơm: dl² = g11 dx² + 2g12 dxdy + g22 dy². V́ mỗi điểm lồi lơm khác nhau bị bao quanh bởi mỗi h́nh b́nh hành khác nhau (không như trường hợp mặt cầu trơn tru chỉ có một h́nh vuông duy nhất ở mọi điểm), nên ba hệ số g11, g12 và g22 không nhất thiết là con số mà là hàm của x, y trong trường hợp chung tổng quát, vậy ta có g11(x, y), g12(x, y), g22(x,y). Suy từ hai chiều sang bốn, ta thấy với không-thời gian bốn chiều cong uốn của h́nh học Riemann, b́nh phương khoảng cách giữa hai điểm kế cận vi phân (xμ và xμ + dxμ) phải là

ds² = gμν(xλ) dxμ dxν (I)

và ta gọi gμν(xλ), hàm của tứ-vectơ xλ, là metric (như mét) đo lường khoảng cách giữa hai không-thời điểm trong cấu trúc h́nh học cong bốn chiều. Sự đối xứng toàn diện trong hoán chuyển μ ↔ ν của ds² bảo cho ta có tất cả mười ^[20] thành phần gμν(xλ) gộp lại trong một đại lượng duy nhất mà ta gọi là ma trận 4×4 g(xλ), cũng như những tứ-vectơ xλ, xμ, xν đều có bốn thành phần x0, x1, x2, x3. Để tóm tắt, trong giai đoạn đầu thai nghén của thuyết tương đối rộng, Einstein đặt nền tảng h́nh học của một không-thời gian cong trong đó khoảng cách b́nh phương giữa những sự kiện vật lư tạo thành những h́nh hyperboloïd ^[21] . H́nh này là quỹ tích của tập hợp các điểm cách trung tâm hệ quy chiếu O một độ dài ds trong thế giới cong bốn chiều, cũng như mặt h́nh cầu là quỹ tích của tập hợp các điểm cách trung tâm O một độ dài |dX| trong thế giới phẳng ba chiều. Cấu trúc cốt lơi của h́nh học cong chính là metric gμν(xλ), một hàm tổng quát của tứ-vectơ xλ. Không có hệ qui chiếu nào ưu tiên hơn hệ khác để diễn tả các hiện tượng vật lư, các định luật vật lư đều phải giữ nguyên dạng trong bất kỳ hệ qui chiếu phi quán tính nào mà ta chọn. Einstein gọi nó là nguyên lư tương đối tổng quát, mở rộng cái nguyên lư tương đối hẹp của Galilei như đă tŕnh bầy ở đoạn 2.

3c. Giai đoạn thứ hai vô cùng quan trọng trong tiến tŕnh xây dựng thuyết tương đối rộng là sự đồng nhất hóa metric gμν(xλ) của cấu trúc h́nh học thuần túy với trọng trường của vật lư. Đó quả thật là một cách mạng trong tư duy khoa học của loài người khi Einstein gắn bó hai đại lượng cơ học và h́nh học mà trước ông ai cũng nghĩ rằng hoàn toàn khác biệt. Nó thể hiện ư tưởng sung sướng nhất đời của Einstein mà ông gọi là nguyên lư tương đương giữa gia tốc và trọng trường đă nói ở trên. Thực thế, chúng ta hăy xem xét một quan sát viên trong hệ quy chiếu quán tính của không-thời gian phẳng bốn chiều Minkowski, người ấy không nhận ra một trọng trường nào cả, mọi vật không rơi mà di chuyển đều đặn hay đứng yên, và thước đo lường khoảng cách không-thời gian là metric đơn sơ ημν. Nay người ấy ở trong thang máy rơi với gia tốc ≠ 0, anh ta thấy hai điều (i) tọa độ không-thời gian sẽ biến đổi một cách phi tuyến tính với metric gμν(xλ) thay đổi từ điểm này sang điểm kia rất phức tạp (ii) mọi vật trong thang rơi nhanh, sự chuyển động có gia tốc này giống như tác động của một trọng trường ảo, vậy metric gμν(xλ) diễn tả trọng trường theo nguyên lư tương đương. Cái gắn bó đồng nhất giữa h́nh học và cơ học, giữa metric và trọng trường đưa ta đến kết luận là hai vật hút nhau chỉ v́ hai vật đó rơi t́m nhau theo con đuờng trắc địa của h́nh học cong diễn tả bởi gμν(xλ). Đường trắc địa ^[22] là con đường tối ưu (ngắn hay dài nhất) nối kết hai điểm A và B với nhau, đó chính là quỹ đạo của hai vật đặt ở A, B chuyển động tự nhiên (chẳng do một lực hút nhau nào tác động lên chúng cả) trong cái thế giới cong bốn chiều của không-thời gian. Dưới ánh đèn huyền ảo của thuyết tương đối rộng, hiện tượng vạn vật hấp dẫn cổ điển "cơ bắp" của Newton nay tỏa hiện như cảnh tượng cong uốn của không gian để làm vật chất rơi t́m nhau!

3d. Giai đoạn cuối cùng trong quá tŕnh xây dựng thuyết này là Einstein truy tầm nguồn gốc của cấu trúc không-thời gian cong, nghĩa là khám phá ra phương tŕnh mà metric h́nh học gμν(xλ) - nay chính là trọng trường - phải tuân theo. Newton đă chứng minh chính khối lượng của một vật, vừa là nguyên nhân tạo ra trọng trường tác động lên vạn vật, cũng vừa là quán tính diễn tả vật ấy chịu sự chi phối của trọng lực tạo ra bởi các vật khác nó. V́ năng lượng cũng là khối lượng (m = E/c²) theo thuyết tương đối hẹp, vậy chính mật độ năng lượng đă tạo ra cái cấu trúc cong của không-thời gian bốn chiều để vạn vật rơi vào nhau theo những đường trắc địa. Hơn nữa, mật độ năng lượng phân phối trong không-thời gian chỉ là một trong mười thành phần của tenxơ năng-xung lượng ^[23] Tμν, vậy tenxơ Tμν này mới chính là nguyên nhân tạo ra metric gμν(xλ) để diễn tả cấu trúc cong của không-thời gian. Chắc chắn chẳng phải ngẫu nhiên mà cả hai đại lượng gμν(xλ) và Tμν đều có đúng mười thành phần đối xứng với hoán chuyển μ↔ν, hệ quả của sự nhất quán giữa toán với vật lư trong cách suy luận và diễn tả.


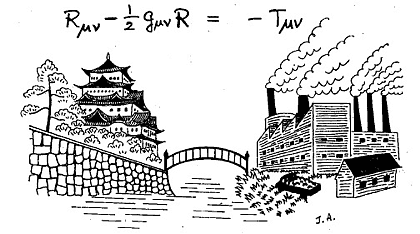
4. Cổng Rashomon và ống khói nhà máy

Lư thuyết tương đối rộng, hay định luật vạn vật hấp dẫn của Einstein ^[24] có thể tóm tắt trong một câu: Không-thời gian chẳng cứng nhắc mà đàn hồi, h́nh học Minkowski bốn chiều phẳng lặng bị biến dạng thành cong uốn bởi năng-khối lượng của vật chất. Chính sự phân phối năng lượng đă tạo ra cấu trúc cong của không-thời gian, nhờ đó vạn vật rơi vào nhau như một biểu hiện của trọng trường chứ không có sức hút nào giữa chúng cả. Ư tưởng vật lư đă thành h́nh, vấn đề c̣n lại của Eintein là t́m ra phương tŕnh toán học để diễn tả sự biến dạng đàn hồi của thế giới phẳng Minkowski. Tính đàn hồi của một vật là khả năng vật đó trở lại trạng thái ban đầu khi mất đi dần lực áp đặt lên nó để làm nó biến dạng, và Robert Hooke ^[25] , nhà bác học Anh (1635-1703) đồng thời với Newton, đă đặt nền móng khảo sát tính chất này với phương tŕnh B = κ T, kư hiệu B chỉ sự biến dạng đàn hồi và T là lực căng làm biến dạng vật. Trong trường hợp không-thời gian bị biến dạng bởi năng-khối lượng, lực căng này chính là tenxơ năng-xung lượng Tμν như đă phân tích ở trên, hệ số tỷ lệ κ nhỏ th́ biến dạng ít, hay 1/κ lớn th́ không-thời gian càng cứng nhắc. Sự t́m kiếm toán tử B làm biến dạng cấu trúc h́nh học phẳng kéo dài trong ba năm gian lao, khởi đầu vào tháng Tám năm 1912, khi Einstein từ chức giáo sư đại học ở Praha để trở về đảm nhận chức vụ giáo sư thực thụ ở trường cũ Bách khoa Công nghệ Zürich (ETH). Tại đây ông đề nghị cộng tác với bạn xưa cùng trường Marcel Grossmann, một nhà toán h́nh học nay là chủ nhiệm khoa toán-lư của ETH trong việc t́m kiếm toán tử B. Nhà toán học Grossmann, không quen thuộc với h́nh học không gian phi thuần nhất (chứa đựng vật chất và năng-xung lượng) mà nhà vật lư Einstein cần đến, bèn tham khảo tài liệu, thư mục và mách bảo cho bạn những điều cần thiết chứa đựng trong công tŕnh của Riemann và những nhà toán học kế tiếp như Christoffel, Ricci và Levi-Civita để Einstein đi từ gμν(xλ) mà xây dựng nên đối tượng toán học B(g_μν(x^λ)) ≡ B_μν. Toán tử Bμν làm biến dạng cấu trúc h́nh học phẳng thành cong không đơn sơ chỉ là sự khác biệt gμν(xλ) – ημν như ta mơ hồ đoán vậy. Thực thế, theo nguyên lư tương đương giữa trọng trường (vật lư) và gia tốc (h́nh học) “sung sướng nhất đời ông” trong cái không-thời gian với cấu trúc tổng quát phức tạp gμν(xλ), ta để thang máy rơi tự do và câu hỏi là trọng trường có thực sự bị xoá bỏ đi ở mọi điểm trong cái thang rơi có gia tốc? Câu trả lời là sự xóa bỏ trọng trường bởi gia tốc không trọn vẹn, hăy c̣n chút đỉnh thặng dư v́ thực ra hai điểm cách nhau vi phân không rơi đồng nhất như hệt nhau với cùng một gia tốc. Điều này thể hiện qua việc metric gμν(xλ) thay đổi từ điểm này sang điểm kia. Cái thặng dư gia tốc đó có thể mường tượng qua thí dụ thủy triều của nước biển sớm tối trào lên và rút đi. Thực vậy nước biển ở phần bán cầu trái đất gần mặt trăng (mặt trời) bị “rơi kéo” vào mặt trăng (mặt trời) với gia tốc khác với gia tốc của nước biển ở bán cầu đối nghịch xa mặt trăng (mặt trời), và sự khác biệt kép ấy chính là nguyên nhân của thủy triều. Vậy làm sao tính cái thặng dư gia tốc ở mỗi thời-không điểm? Mà nói đến sự khác biệt của gμν(xλ) giữa hai điểm vi phân xλ và xλ + dxλ là nói đến đạo hàm, vậy ta không ngạc nhiên khi thấy đạo hàm của gμν(xλ) (như hệ số Christoffel và tenxơ Ricci Rμν diễn tả độ cong của h́nh học Riemann) xuất hiện trong Bμν, và ông t́m thấy Bμν = Rμν – (½)Rgμν, đó là chặng đường vất vả nhất kéo dài ba năm ^[26] . Giai đoạn chót là xác định được hệ số κ trong phương tŕnh Bμν = κTμν. Để t́m nó, định luật hấp dẫn cổ điển của Newton được Einstein khai thác như một dạng xấp xỉ gần đúng ^[27] của phương tŕnh R00 – (½)Rg00 = κT00. Thực thế, thành phần T00 (phụ chú 23) v́ tỷ lệ thuận với mật độ năng lượng E = mc2 nên cũng tỷ lệ với mật độ khối lượng m trong thể tích của một vật nào đó (trái đất chẳng hạn) và chính m tạo ra gia tốc Gm/R2 áp đặt lên các vật khác (ở cách nó một đoạn không gian R) để làm chúng vận hành, và ông xác định được ^[28] hệ số κ = 8πG/c4, G là hằng số Newton của trọng lực. Ngày 25 tháng Mười Một năm 1915, nhà vật lư Einstein sau ba năm lăn lộn với h́nh học đă trao tặng cho nhân loại thuyết tương đối rộng mà ngày nay mang đầy tính thời sự khoa học nóng hổi, từ nghiên cứu cơ bản (vũ trụ và sự h́nh thành, Big Bang, Big Crunch, lỗ đen, siêu dây, năng lượng và vật chất tối, chân không lượng tử, lư thuyết thống nhất toàn thể) đến muôn vàn ứng dụng (thí dụ hệ thống định vị toàn cầu ^[29] mà chúng ta dùng hàng ngày trong các phương tiện di chuyển). Mời bạn đọc chiêm ngưỡng phương tŕnh Einstein mà vế trái mô tả h́nh học không-thời gian bốn chiều trong đó vận hành vạn vật, c̣n vế phải là vật chất xây dựng nên cái cấu trúc cong uốn của không-thời gian:

Rμν – (½)R gμν = (8πG/c4)Tμν (II)

Trong mười thành phần của phương tŕnh Einstein, chỉ có thành phần 00 là tương hợp với định luật cổ điển vạn vật hấp dẫn của Newton (sau khi ta áp dụng phép tính xấp xỉ gần đúng), c̣n chín cái khác là mới. Thông điệp vật lư gói ghém trong phương tŕnh trên có thể tóm tắt như sau: khối lượng áp đặt không-thời gian phải cong đi, c̣n không-thời gian chi phối bắt khối lượng phải chuyển động ra sao. Sự vận hành của vật chất (ánh sáng cũng là vật chất) bởi trọng trường không do một lực cơ bắp nào hết mà thực ra sự di chuyển đó lại ‘trây lười nhất’ theo đường trắc địa trong một không-thời gian bị cong bởi sự hiện hữu và phân phối của vật chất. Đáp lại, vật chất và năng lượng luôn luôn biến chuyển của chúng cũng tác động tới độ cong của không-thời gian, và cứ thế tiếp diễn liên hồi vũ điệu giữa cơ học và h́nh học. Mật độ năng-xung lượng càng lớn ở đâu th́ không-thời gian cong uốn càng nhiều ở đấy, đó là gốc nguồn của lỗ đen, một không-thời gian tận thế ở đó bất kỳ vật chất nào, kể cả ánh sáng và tín hiệu thông tin, khi đi gần đều bị hút chặt vào chẳng sao thoát khỏi. Mời bạn đọc coi bức thư ông gửi ngày mồng 9 tháng giêng năm 1916 cho Karl Schwarzschild (nhà vật lư thiên văn Đức đang hành quân ở mặt trận Nga - Đức trong Thế giới Đại chiến 1914-1918, vào những giờ phút ngừng bắn đă đầu tiên giải được chính xác phương tŕnh của thuyết tương đối rộng mà Einstein vừa công bố tháng trước): “Cái đặc điểm của lư thuyết mới này là không gian và thời gian tự chúng chẳng có tính chất vật lư ǵ cả. Nói đùa thôi, giả thử mọi vật trên đời biến mất, th́ theo Newton ta hăy c̣n một không gian rỗng tuếch phẳng lặng mênh mang và mũi tên thời gian vẫn lặng lẽ trôi, nhưng theo tôi th́ tuyệt nhiên chẳng c̣n chi hết, cả không gian lẫn thời gian và vật chất ^[30] !” Thực là một cuộc cách mạng về tư duy mà Einstein mang đến cho nhân loại: chính vật chất trong đó có da thịt tâm tư con người xây dựng ra vũ trụ. Vật chất và không-thời gian chỉ là hai khía cạnh của một bản thể duy nhất, cái này sinh cái kia, không có cái này th́ cũng chẳng có cái kia. Nhà vật lư Nhật bản Yoichiro Nambu ^[31] qua bức tranh nửa trào lộng nửa trầm tư minh họa vế trái phương tŕnh Einstein bằng cổng Rashomon xa xưa của một thoáng không gian thanh thoát bên bờ suối, c̣n vế phải bên kia cầu vương vấn trong cảnh trần ai bởi khói than nhà máy phản ánh vật chất nặng nề!



Ngay sau khi khám phá ra phương tŕnh (II) của thuyết tương đối rộng, Einstein đề xướng hai phương thức để kiểm chứng thuyết đó bằng thực nghiệm ^[32] . Để đánh giá phần nào gia tài tri thức mà Einstein trao cho nhân loại, mời bạn đọc nhớ lại vào cuối thế kỷ 19, khoa học thời "tiền tương đối” được hiểu như sau: Không gian ba chiều như một sự thực tiên nghiệm ‘trời cho’, một sân khấu lạnh lùng hoàn toàn biệt lập với vật chất thao diễn trong đó. Cấu trúc h́nh học của không gian phẳng (tổng cộng ba góc h́nh tam giác bằng 180 độ) đă được khai thông bởi các nhà hiền triết Hy Lạp Euclid, Pythagoras từ hơn hai thiên niên kỷ. Thời gian như một mạch đập "hiện sinh” của vũ trụ, một mũi tên lặng lẽ trôi vô thủy vô chung. Vật chất là một thực thể thường trực vĩnh viễn không sinh không hủy, và sau hết lực tác động tức thời lên vật chất làm chúng vận hành. Einstein đă cho ta một nhận thức khoa học và triết học khác: bước chuyển thời gian là một ảo tưởng, chỉ có một thực tại duy nhất không-thời gian bốn chiều gắn bó với nhau, chẳng có cái "bây giờ”. Vạn vật phù du, vô thường hằng, không ngừng đổi biến. Hơn nữa toàn bộ không gian, thời gian, lực, vật chất chẳng sao tách biệt, cặp không-thời gian (cái vỏ chứa) và cặp lực-vật chất (cái được chứa) chồng chéo liên kết bên nhau, cấu trúc không phẳng mà cong uốn của vỏ được xây dựng bởi chính cái nội dung chứa đựng trong vỏ. Năng lượng là gốc nguồn chung cho tất cả, từ đó vật chất, lực, không gian, thời gian được tạo dựng nên.

© 2008 talawas

^[1]Chất liệu giả tưởng trong đó dao động sóng ánh sáng, chất liệu ấy phải trải rộng khắp vũ trụ, đâu cũng có, v́ ánh sáng đến với ta từ những thiên thể xa xăm. Định kiến (trước năm thần kỳ 1905) cho rằng phải có một chất liệu ether để nhờ đó sóng ánh sáng mới truyền đi được (như sóng nước phải có nước, sóng âm thanh phải có không khí) đă ăn sâu vào tâm khảm mọi người - kể cả Maxwell, người khai phá ra lư thuyết điện từ và chứng minh ánh sáng là sóng điện từ - không ai tin rằng sóng điện từ có thể truyền đi trong chân không mà nhờ Einstein ta biết (xem phần 3a và các phụ chú từ 9 đến 16 về những điều cơ bản của thuyết tương đối hẹp).
^[2]Trớ trêu thay, Johannes Stark cũng như Philipp Lenard (người khám phá ra hiệu ứng quang điện mà cũng lại Einstein giải thích năm 1905 bằng thuyết lượng tử) sau này theo chủ nghĩa cực đoan phát xít, đánh phá mạnh mẽ Einstein, con người của lương tâm và trí tuệ, của tự do dân chủ, ngay từ trước Thế giới Đại chiến thứ Nhất (1914-1918) đă chống chủ nghĩa quốc gia dân tộc và tôn giáo hẹp ḥi, nh́n xa đề xướng một Âu châu ḥa hợp. Lịch sử từng chứng kiến chuyện đánh phá trí thức bởi đồng nghiệp như thời Staline bên Liên Xô, McCarthy bên Mỹ, Cách mạng Văn hóa của Mao bên Trung Quốc. Việt Nam cũng không là ngoại lệ!
^[3]Chuyện kể Galilei đứng trên đỉnh tháp nghiêng của thành phố Pisa, thấy đá và giấy rơi hệt như nhau rồi phát hiện ra tính chất phổ quát chỉ là huyền thoại, thực ra ông làm thí nghiệm trên những mặt phẳng nghiêng mà suy luận ra tính phổ quát nói trên.
^[4]Trọng lượng của A là sức hút (hay trọng lực) F của trái đất - hay của mặt trăng, tinh tú hoặc bất kỳ vật B nào khác A - áp đặt lên A. Nếu M là khối lượng của vật B (trái đất chẳng hạn) và m là khối lượng của vật A, th́ theo Newton, trọng lực F của B áp đặt lên A bằng GMm/ R2, với R là khoảng cách không gian giữa A và B, G là hằng số hấp dẫn Newton. Nói cách khác, B tạo ra một trọng trường để lôi hút mọi vật về nó. Trường (tỏa rộng khắp không gian và thay đổi với thời gian để diễn tả tác động của lực) là một khái niệm sâu sắc của vật lư mà trực giác của Faraday (một nhà thực nghiệm xuất chúng, tự học, làm thợ in để sinh sống mà chỉ mê say nghiên cứu khoa học) nhận ra khi ông nh́n những vụn sắt trải đều đặn chung quanh hai trục bắc nam của thanh nam châm. Điện tích di chuyển sinh ra điện từ trường, c̣n khối lượng tạo ra trọng trường.
^[5]Thực ra ở thời điểm Galilei và Newton, người ta tưởng rằng có hai loại khối lượng m và m’ khác nhau, m diễn tả khối lượng để tạo ra trọng trường trong công thức GMm/ R2, c̣n m’ (trong phương tŕnh cơ bản của động lực học F = m’γ) là khối lượng diễn tả khả năng trây ỳ của vật thể chống lại sự di chuyển do bất kỳ lực F nào (không nhất thiết phải là trọng lực) áp đặt lên nó. Tính phổ quát của Galilei được Newton minh giảng bằng giả thuyết m = m’ (xem phụ chú 6). Giả thuyết m = m’ được chứng nghiệm bởi nam tước von EötVös vào cuối thế kỷ 19 với sai số 10−9, ngày nay sai số giảm xuống 10−12.
^[6]Thực thế, trọng lượng F = GMm/ R2 của A (nghĩa là lực tạo nên bởi trọng trường của trái đất áp đặt lên A) tỉ lệ thuận với m, khi kết hợp với phương tŕnh cơ bản của động lực học F = m’γ = m γ mà Newton phát hiện năm 1686, cho ta thấy gia tốc γ = GM/ R2 chuyển vận của A không phụ thuộc vào khối lượng m của nó nữa, đó là tính phổ quát của trọng trường mà Galilei t́m ra. Thay v́ γ, các sách giáo khoa thường hay dùng kư hiệu g (gravitation) để chỉ định gia tốc chung cho mọi vật hút bởi trọng trường của trái đất. Đo được g ≈ 9. 81 m/s2 là gián tiếp đo được khối lượng khổng lồ M ≈ 5.97 × 1024 kg của quả địa cầu (thực nghiệm của Henry Cavendish năm 1798). Trái lại điệntừ trường E và H áp đặt lên một vật thể (mang điện tích q) làm cho nó chuyển động với gia tốc thay đổi theo khối lượng m của vật ấy. Thực thế, lực điện-từ f = q (E + V× H), khi kết hợp với f = mγ làm cho vật chuyển động với gia tốc γ ~ q/m. C̣n trong thế giới vi mô hạ nguyên tử, lực mạnh (sắc động lực học luợng tử tác động lên các hạt cơ bản quark để làm chúng gắn kết với nhau thành hạt nhân nguyên tử) lại chẳng giống trọng lực hay điện từ lực chút nào. Lực mạnh tăng lên với khoảng cách r giữa hai quark, trong khi lực cổ điển của thế giới vĩ mô (trọng lực và điện-từ) giảm đi như 1/ r2 .
^[7]Sự đối xứng, hoán chuyển toàn diện giữa M và m trong sức hút lẫn nhau F = GMm/ R2 của hai vật A và B cho ta thấy ngay chính A cũng tác động lên B làm cho B di chuyển với gia tốc Gm/ R2 và ngược lại trọng trường tạo ra bởi B làm cho A vận chuyển với gia tốc GM/ R2 .
^[8]Như tác giả kể lại, so với gian lao "siêu phàm", lời của ông, trong việc sáng tạo ra thuyết tương đối rộng th́ thuyết tương đối hẹp (với những kết quả kỳ diệu như E = mc2 , thời gian dăn nở, không gian co cụm trong những hệ quy chiếu di động đều đặn) chỉ là tṛ con trẻ mà ông khám phá ra trong có một buổi chiều Chủ nhật tháng Năm năm 1905, sau bữa dạo chơi và tṛ chuyện về bí hiểm ether với anh bạn thân thiết Michele Besso cùng sở làm ở thành phố Bern.
^[9] Hệ quy chiếu quán tính là hệ quy chiếu di chuyển với vận tốc v đều đặn, cố định với thời gian (gia tốc = 0), kể cả v = 0, kư hiệu in đậm v chỉ định vectơ vận tốc ba chiều không gian, và v ≡ |v|. Từ nay các vectơ ba chiều đều được viết dưới dạng in đậm như k, x … và k = |k|, x = |x|…
^[10]Ai trong chúng ta khi đi máy bay cửa sổ đóng kín và không gặp băo lay động mà có thể cảm thấy ḿnh di chuyển với vận tốc khoảng ngàn cây số trong một giờ? Khoảng bốn trăm năm trước đây, Galilei cũng đưa ra một thí dụ tương tự, mở đầu cho nguyên lư tương đối mang tên ông: trong hầm kín mít không giao tiếp ǵ với thế giới bên ngoài của một chiếc tàu thủy di chuyển đều đặn, ta hăy quan sát những con bướm bay khắp phía và những giọt nước tí tách rơi. Nay để tàu đứng yên, ta thấy bướm vẫn bay và nước vẫn rơi hệt như trước, chẳng có ǵ thay đổi. Rồi tàu lại di chuyển đều đặn, nhưng với vận tốc và chiều hướng khác, bướm vẫn bay và nước vẫn rơi như khi tàu dừng ở bến. Nói một cách khác: những định luật miêu tả các hiện tượng thiên nhiên (bướm bay, nước rơi) không chút thay đổi ǵ trên tàu di chuyển đều đặn (bất kỳ vận tốc và chiều hướng nào) kể cả tàu dừng ở bến (v = 0). Người ở trong tàu nếu chỉ quan sát đo lường những hiện tượng động hay tĩnh trong tàu mà không tiếp xúc với bên ngoài để so sánh th́ chẳng sao biết là tàu đứng hay đi, và đi với vận tốc nào, chiều hướng nào. Nói khác đi, tĩnh hay di động đều đặn chỉ là chuyện tương đối, chẳng có lư ǵ để khẳng định bến hay tàu, cái nào đứng, cái nào đi.
^[11](x,y,z,t) chỉ định toạ độ không gian-thời gian bốn chiều của một hiện tượng vật lư xẩy ra trong hệ quy chiếu đứng yên, c̣n (x’,y’,z’,t’) trong hệ quy chiếu di chuyển với vận tốc đều đặn v so sánh với (x,y,z,t).
^[12]Các tọa độ bốn chiều (x,y,z,t) và (x’,y‘, z’,t’) của hai hệ quy chiếu phải liên hệ ra sao để làm cho hàm f(x,y,z,t) nói trong bài, nay gọi là đại lượng s² = (x² + y² + z²) - (ct)² = (x’² +y’² +z’²) - (ct’)² không thay đổi, nghĩa là s² bất biến. Sự bất biến của s² diễn tả hiện tượng vật lư theo đó vận tốc ánh sáng c ~ 300000 km/s đo lường trên hai hệ quy chiếu (một đứng yên mà ta gọi là trên bến, một di chuyển với bất kỳ vận tốc v nào mà ta gọi là dưới tàu) đều bằng nhau và là c cả. Thực thế khi s² = 0, c = r/t = ± r’/t’ (với r² = x² + y² + z²), dấu ± để chỉ ánh sáng chạy cùng hay ngược chiều trong hai hệ quy chiếu. Hiện tượng này do Michelson và Morley phát hiện năm 1887, nó trái ngược với trực giác và định kiến của mọi người trước năm thần kỳ 1905 v́ họ tưởng (nhầm) rằng nếu vận tốc ánh sáng đo trên bến là c th́ đối với người trên bến vận tốc ánh sáng đo trên tàu phải là c ± v (tùy theo ánh sáng chạy song song cùng chiều hay ngược chiều với tàu). Cũng vậy, người trên tàu khi đo vận tốc ánh sáng sẽ thấy vận tốc đó phải khác với vận tốc ánh sáng truyền đi trên bến, sự khác biệt đó cho ta v. Nay ta hăy thay bến bằng ether (một chất liệu giả tưởng trải rộng khắp vũ trụ nhờ đó sóng điện từ nói chung và ánh sáng nói riêng truyền đi, như vậy ether được coi như một hệ quy chiếu hoàn toàn bất động), và thay tàu bằng trái đất di động. Michelson và Morley khi so sánh vận tốc ánh sáng phát ra theo hai chiều đối ngược nhau trên trái đất, nghĩ sẽ đo được vận tốc v của làn gió ether thổi so với trái đất coi như đứng yên. Nhưng hai ông sau bao lần đo lường thấy vận tốc ánh sáng lúc nào cũng vẫn bằng nhau, và như vậy không sao phát hiện nổi sự hiện hữu của ether. Đó là nghịch lư của cơ học cổ điển Galilei-Newton với định kiến chỉ có một thời gian phổ quát (t’ = t) và một không gian tuyệt đối chẳng mảy may liên hệ với thời gian. Thực thế - trường hợp vận tốc v song song cùng chiều với trục Ox - cơ học cổ điển cho ta x’ = x – vt, y’ = y, z’ = z, t’ = t như vậy th́ s² không sao bất biến được. Trái lại phép hoán chuyển Lorentz x’= k (x- vt), y’ = y, z’ = z, t’ = k (t –(xv/c²)), với k = 1 ⁄ √(1− v² ⁄c²) làm cho s² bất biến. Giải đáp nghịch lư này bằng nguyên lư tương đối áp dụng cho sự vận hành của ánh sáng là gốc nguồn của lư thuyết tương đối hẹp mà Einstein, Lorentz, Poincaré đă đóng góp vào. Nếu w là vận tốc của vật chuyển động trên tàu, th́ - đối với người đứng trên bến - luật cộng trừ vận tốc w ± v (cơ học cổ điển cho ta) chỉ là dạng xấp xỉ gần đúng và phải được thay thế bởi công thức (w ± v)/(1 ± w v/c²). Bạn đọc sẽ ngạc nhiên và thích thú nhận thấy khi w = c, công thức (w ± v)/(1 ± w v/c²) không c̣n tùy thuộc vào v nữa mà lúc nào cũng bằng c, minh hoạ thực nghiệm của Michelson và Morley.
^[13]Mà ta có thể ‘đoán’ được k qua s²: s² = r² – (ct)² = r’² – (ct’)². Thực thế thời gian t’ chỉ định bởi đồng hồ di động đặt ở vị trí x’, y’, z’ ( r’ = 0), cho ta ct’– 0 = (ct)√(1 – r²/t²c²) = (ct)√(1– v²/c²), do đó t = kt’. Đồng hồ trong tàu di động chỉ một giây, người ở ngoài thấy dài hơn một giây, đồng hồ ở trong tàu như chạy chậm lại.
^[14]Một gam khối lượng tuy nhỏ nhưng tiềm ẩn một năng lượng khổng lồ tương đương với nhu cầu dinh dưỡng của vài chục ngàn người trong vài năm! Từ hệ số k = 1 ⁄ √(1− v² ⁄c²) ông nhận ra là khối lượng m của một vật không cố định mà tăng lên với vận tốc của nó, m(v) = m ⁄ √(1− v² ⁄c²). Khi triển khai hạn chế theo (v² ⁄c²) «1, m(v) = m + [1/c²] (½)mv² +… mà (½)mv² chính là động năng quen thuộc của cơ học, Einstein đă t́m ra công thức của thế kỷ E = mc²/√(1− v² ⁄c²) công bố tháng 10 năm 1905. Cũng trong bài báo đó ông c̣n b́nh giải ư nghĩa vật lư của công thức: khối lượng m (của bất kỳ một vật chất nào) chỉ là sự tích tụ năng lượng E (chia cho c²) của vật đó (khi nó không di động, v = 0). Phương tŕnh E = mc²/√(1− v² ⁄c²) quả là một thay đổi cách mạng trong sự hiểu biết và nhận thức về vật chất: năng lượng và khối lượng cùng chung một bản thể. Đặc biệt ánh sáng thuần tuư (năng lượng) có thể tạo ra vật chất ! Ngoài ra ông c̣n đề xuất phương cách kiểm chứng E = mc² bằng thực nghiệm, một vật - chẳng hạn hạt nhân radium phóng xạ tự nhiên - khi mất đi (hay thu nhận) một chút năng lượng δE th́ khối lượng nó giảm đi (hay tăng lên) δE/c².
^[15]Thuyết tương đối hẹp bảo cho ta trên các hệ quy chiếu di chuyển với vận tốc v, thước đo không gian (theo hướng song song với v) bị co cụm lại với hệ số 1/k = √(1− v² ⁄c²), trái lại (theo hướng thẳng góc với v) thước đo không thay đổi. Cũng thế khoảng cách thời gian dăn nở ra với hệ số k, hay là nhịp độ tích tắc đồng hồ đập chậm đi k lần trong một đơn vị thời gian. Trên vệ tinh của Hệ thống Định vị Toàn cầu (Global Positioning System, GPS) trang bị các phương tiện vận tải, sự chính xác cực kỳ của nhịp độ đồng hồ là điều kiện tối quan trọng cho GPS thành công. Bạn đọc sẽ thấy ở các vệ tinh GPS, thuyết tương đối rộng cho ta hệ quả ngược với thuyết tương đối hẹp, khoảng cách thời gian co cụm lại (đồng hồ tích tắc nhanh hơn) v́ cường độ trọng lực trên đó giảm đi so với mặt đất. Sự co dăn thời gian (nhịp độ đồng hồ) của các vật chuyển động khác nhau đă được thực nghiệm kiểm chứng nhiều lần với độ chính xác cực kỳ, tiếp nối bởi biết bao ứng dụng thực tiễn trong đời sống con người .
^[16]Người bạn thân thiết nhất từ thuở hàn vi, người duy nhất ông cảm ơn trong công tŕnh để đời đăng trên Annalen der Physik về thuyết tương đối hẹp trong lúc hai người dạo chơi bàn luận ngày Chủ nhật tháng Năm năm 1905, trong bài đó ông không hề trích dẫn một tài liệu tham khảo nào mặc dầu lúc ấy chẳng ai biết đến ông, đủ thấy cá tính con người siêu việt này. Chữ "gläubige" trong bức thư không nên hiểu theo nghĩa tín ngưỡng tôn giáo, mà hàm ư xác tín vào lư trí. Bức thư gửi chưa đến một tháng th́ Einstein cũng vào cơi vĩnh hằng.
^[17]Tựa như đường thẳng (quỹ đạo của hạt di chuyển không gia tốc) biến dạng ra các h́nh conic (quỹ đạo của hạt di chuyển có gia tốc), hay h́nh cầu của bóng đá biến dạng ra bóng bầu dục (ellipsoïd) v́ tác động của trọng lực. H́nh học cong này có thể nhận ra khi ta đứng yên quan sát một người ở trong một sàn quay chung quanh trục thẳng góc với sàn. Anh ta đo chu vi của sàn sẽ thấy lớn hơn π ≈ 3.14 lần đường kính của sàn. Thực thế, vận tốc v của sàn quay tiếp tuyến với chu vi của nó, vậy thước đo chiều dài chu vi sàn bị co lại (phụ chú 15), trong khi đường kính sàn v́ thẳng góc với v nên thước không co. Ṿng tṛn trong h́nh học phẳng có chu vi bằng π đường kính của nó, nhưng trong h́nh học cong v́ thước đo chu vi co cụm nên chu vi lớn hơn π đường kính.
^[18]Khi viết Aμ Bμ hay Aμν Bμν (với một hay nhiều chỉ số cái trên, cái dưới ), th́ ta phải cộng tất cả các đóng góp của chỉ số lại, thí dụ Aμ Bμ = A0 B0 + A1 B1 + A2 B2 + A3 B3, ημν dxμ dxν = ηoo dx0 dx0 + ηi i dxidxi + η0i dx0 dxi + ηij dxidxj (i, j = 1,2,3 và i≠j). Xin nhớ rằng tuy Aμ , Bμ hay Aμν, Bμν đều là những vectơ hay tenxơ mang nhiều thành phần, quy ước tổng hợp Riemann-Einstein cho ta Aμ Bμ hay Aμν Bμν chỉ có một thành phần duy nhất, nó là một đối tượng h́nh học vô hướng (scalar).
^[19]Gauss mới khoảng mươi tuổi trong lớp tiểu học, để giữ cho học tṛ khỏi quấy, ông giáo cho bài toán sau đây: tính tổng số của một trăm số nguyên 1+2+…+100. Trong khi cả lớp loay hoay cộng dần vài số và kiểm điểm từng đoạn tính toán cho chắc, Gauss nh́n trăm số nguyên một cách tổng quát, thấy từng cặp số đầu (1) + số cuối (100) cũng như số thứ nh́ (2) + số áp cuối (99), 3 + 98 vân vân, tất cả 50 cặp đều như nhau và bằng 101. Vậy chỉ vài phút sau , cậu bé Carl Friedrich hănh diện mang đáp số 101x50 =5050, trước nỗi kinh ngạc của cả lớp từ thầy đến bạn. Tên ông cũng gắn liền với đơn vị cường độ từ trường, với định lư Gauss dùng trong điện tĩnh. Để mua vui bạn đọc, xin nhắc đến một thần đồng nước ta, Lê Quư Đôn, sinh trước Gauss, với bài thơ tạ lỗi v́ cậu dạng chân tay trần truồng (giống chữ Thái trong Hán tự) để đố bạn cha ḿnh là chữ ǵ (ông bạn tưởng là chữ Đại), hai chữ Thái và Đại viết khác nhau chỉ có một cái chấm mà riêng con trai mới có. Cái độc đáo là mỗi câu thơ mang tên một con rắn: “Chẳng phải liu điu vẫn giống nhà, Rắn đầu biếng học lẽ không tha, Thẹn đèn hổ lửa đau ḷng mẹ, Nay thét mai gầm rát cổ cha, Ráo mép chỉ quen tuồng dối trá, Lằn lưng cam chịu vết roi cha, Từ nay trâu lỗ xin siêng học, Kẻo hổ mang danh tiếng thế gia.”
^[20]Mỗi hệ số μ, ν có 4 giá trị 0, 1, 2, 3, vậy ma trận 4×4 gμν có 4 × (4 + 1)/2 = 10 thành phần đối xứng trong hoán chuyển μ↔ ν , và 4 × (4 − 1) )/2 = 6 thành phần bất đối xứng.
^[21]Khi tất cả 10 gμν đều cùng dấu ta có bóng bầu dục (ellipsoïde, đề tài của Riemann), khi gμν có dấu khác nhau như trường hợp ημν, ta có h́nh hyperboloïd mà Einstein nghiên cứu.
^[22]Đường trắc địa trên bề mặt quả cầu là những h́nh tṛn lớn (cùng đường kính với quả cầu). Trong h́nh học Minkowski v́ ημν mang dấu ±1 nên cạnh AC (trên trục thời gian) của tam giác ABC lại dài hơn tổng cộng hai cạnh AB + BC, và đường thẳng trắc địa nối A và C lại là đường dài nhất. Điều kiện để con đường ŁAB = ∫BA ds (diễn tả bởi sự di chuyển của điểm xλ = xλ (s), thông số s đo độ dài trên con đường) có chiều dài tối ưu là xλ (s) phải tuân theo phương tŕnh vi phân bậc hai:
d²xλ /ds² + Γλμν [dxμ /ds] [dxν/ds] = 0 (1)
Đại lượng Γλμν (hệ số Christoffel) trong phương tŕnh (1) là những đạo hàm của metric gμν(xλ), tính theo công thức sau (với định nghĩa ∂μ gνσ ≡ dgνσ /dxμ )
Γλμν = (½) gλσ [∂μ gνσ + ∂ν gμσ ≡ ∂σ gμν] (2)
^[23]Có 40 = 4 × 10 hệ số Christoffel Γλμν (4 từ λ, 10 từ μν), và gλσ là ma trận nghịch đảo của gλσ (gλα gλβ = δα β, kư hiệu Kronecker δα β = 0 khi α ≠ β và = 1 khi α = β ). Trong h́nh học phẳng Minkowski không gia tốc, v́ metric ημν giản đơn chỉ là những con số ±1 nên theo (2) hệ số Christoffel Γλμν = 0, vậy (1) rút gọn thành d²xλ /ds² = 0, do đó xλ (s) = aλ s + bλ , chứng tỏ đường trắc địa trong h́nh học phẳng là đường thẳng.
Sự liên kết ct với vectơ không gian ba chiều x tạo ra tứ-vectơ không-thời gian xμ (ct, x), một đối tượng bốn thành phần, thường xuyên dùng trong thuyết tương đối hẹp. Cũng vậy năng lượng E và xung lượng (p = mv) liên kết thành tứ -vectơ năng-xung lượng với bốn thành phần: pμ (E, cp). Từ pμ ta xây dựng tenxơ năng-xung lượng Tμν, một ma trận 4×4 (đối xứng μ ≡ ν) mà 4 thành phần đường chéo là mật độ năng lượng E và áp suất P (tỉ lệ với xung lượng p), cùng 6 thành phần hỗn hợp giữa E với áp suất P. Sau chót ta định nghĩa Tμν ≡ gμα gνβ Tαβ, và T00 ~ E = kmc2.
^[24]Thuyết tương đối rộng của Einstein thay thế và bổ sung cho định luật vạn vật hấp dẫn của Newton, thuyết cổ điển này chỉ là trường hợp xấp xỉ gần đúng của thuyết Einstein khi mật độ vật chất nhỏ (trọng trường yếu).
^[25]Tổng thư kư Hàn lâm Viện Hoàng gia Anh, nhà thực vật học đầu tiên phát hiện ra tế bào, nhà thiên văn lỗi lạc có nhiều công tŕnh phong phú (dự đoán luật hấp dẫn 1/ r² và động lực học) nhưng bị thiên tài Newton áp đảo nên ít được hậu thế nhắc đến. Ḷ xo một đầu buộc chặt vào tường, đầu kia kéo dài bởi một quả cân là thí dụ điển h́nh của hiện tượng đàn hồi, sự biến dạng sẽ từ từ mất đi khi lực căng nhỏ dần.
^[26]Tenxơ Ricci Rμν lấy từ những hệ số Christoffel như sau: Rμν ≡ ∂α Γαμν – ∂ν Γαμα + Γαβα Γβμν – Γαβν Γβμα. Sau hết khi nhân ma trận gμν (nghịch đảo của gμν) với Rμν, ta có một đại lượng vô hướng R ≡ gμν Rμν. Chính đại lượng R (mà riêng Einstein đă t́m ra và đặt thêm vào Rμν ngày 25/11/1915) này đóng vai tṛ cần thiết để tương thích với luật bảo toàn năng lượng mà Tμν phải tuân theo. Trước đó năm 1913 khi Grossmann và Einstein cộng tác, hai người đă đi gần tới đích với Bμν = Rμν không thôi.
^[27]Trường hợp trọng trường yếu (mật độ năng khối lượng nhỏ như hệ mặt trời), metric gμν không khác metric phẳng ημν bao nhiêu : gμν(x) = ημν + hμν(x), với x = |x|, và |hμν(x)| « 1, hμν(x) thay đổi chậm chạp cũng như Tij « T0i «T00 (xung lượng p = mv ≈ 0). Phương tŕnh trội nhất R00 – (½)R g00 = (8πG/c4)T00 cho ta luật của Newton: h00(x) = 2GM/(c2x) ≡ 2 U(x)/c2 ≈ 10–9, M là khối lượng trái đất, x là khoảng cách từ tâm quả đất đến vật mà ta khảo sát, và U(x) = GM/x là thế hút của trái đất làm cho vật rơi với gia tốc g = –dU(x)/dx ≈ 9. 81m/s2.
^[28]Trong hệ thống đơn vị đo lường mét (m), kilogram (kg), giây (s), G = 6.67×10–11 và κ ≈ 2 ×10–43 quá nhỏ, không gian quá cứng nhắc khiến ta hiểu tại sao xưa nay chẳng ai ngờ nó bị uốn cong bởi vật chất, chỉ ở đâu và khi nào có mật độ năng lượng lớn vô vàn mới biến dạng độ phẳng lặng của không-thời gian.
^[29]Tần số N -nhịp độ tích tắc của đồng hồ (đặt ở điểm x) - thay đổi với cường độ của trọng trường v́ metric g00(x) thay đổi với x, không cố định như η00: g00(x) = η00 + GM/(c2x) ≡ –1 + 2 U(x)/c2 (phụ chú 27). Đó chính là ư nghĩa của thời gian cong. Xin nhớ g00(x) là hệ số của (cdt)2 trong phương tŕnh (I) nên ta suy từ đó ra mối liên đới giữa tần số N và g00(x):
N1/N2 = [g00(x2)/ g00(x1)]½ ≈ 1+ (1/c2) [U(x1) – U(x2)] (3)
Ở trên các vệ tinh GPS (điểm x1), cường độ trọng trường nhỏ hơn so với mặt đất (điểm x2), U(x1) < U(x2), vậy theo (3) N1 < N2, thời gian như co lại (nhịp độ tích tắc đồng hồ chạy nhanh hơn) trên các vệ tinh GPS. Cũng trên các vệ tinh này di chuyển với vận tốc v so với dưới đất, thời gian trên đó lại dăn nở ra (nhịp độ tích tắc đồng hồ chạy chậm lại) theo thuyết tương đối hẹp. Tác động của thuyết tương đối rộng và hẹp về nhịp độ thời gian đối nghịch nhau nhưng không hoàn toàn triệt tiêu trên vệ tinh, và nhu liệu máy tính được gắn trong GPS để phối hợp hai hệ quả đó. Sự co dăn thời gian trên các vệ tinh GPS được ước tính vào khoảng một phần tỷ (10–9), tuy nhỏ vậy nhưng cực kỳ quan trọng v́ hệ thống định vị toàn cầu đ̣i hỏi sự chính xác bền vững đến một phần mười ngàn tỷ (10–13) của đồng hồ nguyên tử. Theo thuyết tương đối rộng, hai anh em sinh đôi một ở trên núi cao, một ở dưới đồng bằng, người ở dưới (v́ trọng trường lớn hơn so với trên núi) thấy thời gian dăn nở ra hay đồng hồ chạy chậm lại và như vậy trẻ hơn người ở trên cao (một giây trong trăm năm!). Hiệu ứng Einstein về thời gian co dăn bởi trọng trường được kiểm chứng nhiều lần trên các hỏa tiễn bay cách xa mặt đất khoảng 10000 km, ở đấy đồng hồ chạy nhanh hơn độ 4.10–9 giây.
^[30]Thực ra khi vắng vật chất (Tμν = 0), không-thời gian chỉ mất đi cấu trúc cong thôi, ta vẫn c̣n chẳng những không-thời gian phẳng của Minkowski mà cả muôn vàn sóng trọng trường dao động trong một không-thời gian rỗng tuếch phi vật chất chẳng do đâu tạo ra cả. Không-thời gian chỉ thực sự biến mất (khi Tμν = 0) nếu ông thêm vào vế trái của phương tŕnh (II) một số hạng mới Λgμν và ông gọi Λ > 0 là hằng số vũ trụ. Tuy nhiên cái nội dung sâu sắc của bức thư là Einstein nhấn mạnh đến sự liên đới chẳng sao tách biệt giữa vật chất, lực, năng lượng, không gian, thời gian; một cách mạng trong nhận thức.
^[31]Bài tổng kết trong hội thảo quốc tế về vật lư hạt cơ bản và năng lượng cao, Tokyo, 1978.
^[32]Hai kiểm chứng là:
(a) khối lượng mặt trời tạo ra xung quanh nó một không gian cong uốn để cuộn khúc quỹ đạo của hành tinh gần mặt trời nhất - tức Thủy tinh - làm cho hành tinh này lại đến trước một tí chút 43’’ trong một thế kỷ (hiện tượng tuế sai) so với thời điểm mà thuyết hấp dẫn cổ điển của Newton chỉ định. Nhà thiên văn Pháp Le Verrier năm 1859 - dùng thuyết cổ điển Newton - khi tính toán chu kỳ Thủy tinh đă phát hiện ra sự tuế sai nhưng ông không sao giải thích nổi. Einstein - qua phép tính xấp xỉ bậc hai của phương tŕnh (II) - tính toán ra độ cong không gian bởi khối lượng mặt trời, độ cong đó tác động lên chu kỳ của Thủy tinh và ông t́m ra đúng con số 43’’ thần diệu khiến tim ông dữ dội đập như ông về sau kể lại cho bạn bè. Những hành tinh khác v́ ở xa mặt trời nên chẳng mấy bị ảnh hưởng bởi độ cong không gian quá nhỏ, ở xa mặt trời thuyết hấp dẫn cổ điển của Newton rất chính xác và Le Verrier tháng Tám năm 1846 đă tiên đoán sự hiện hữu của Hải vương tinh mầu xanh lơ rất đẹp mà ngay đêm 23 tháng Chín năm ấy đă được đầu tiên nh́n thấy trên bầu trời nước Pháp.
(b) Cũng như mọi vật chất khác, ánh sáng từ một thiên thể xa xăm đến với ta sẽ bị uốn cong khi đi gần mặt trời. Để quan sát được tia ánh sáng bị bẻ cong đó ta cần mặt trăng che lấp mặt trời (nhật thực) rồi so với ánh sáng ban đêm (không có mặt trời) đến từ cùng một thiên thể. Sự khác biệt (giữa ban ngày nhật thực và ban đêm) của tia ánh sáng cho ta biết không gian bị uốn cong bao nhiêu bởi khối lượng mặt trời. Thuyết tương đối rộng tiên đoán độ cong phải bằng 1.75’’ và hai phái đoàn của Hàn lâm Viện Hoàng gia Anh được gửi đi Brasil và đảo Principe để quan sát ánh sáng bị bẻ cong nhân dịp nhật thực ngày 29 tháng Năm năm 1919. Kết quả đo lường đúng như Einstein tiên đoán và sau buổi họp vô cùng căng thẳng và xúc động ngày 6 tháng Mười Một năm 1919 của Hàn lâm Viện Hoàng gia Anh, báo chí khắp nơi trên thế giới đưa tin này (Newton nhường ngôi, Einstein đăng quang!) làm ông bỗng nhiên một sớm lừng danh trong đại chúng, mặc dầu thời ấy tin đồn chỉ có ba người trên thế giới hiểu được thuyết tương đối rộng!

 

5. Hiện t́nh và triển vọng

Dẫu mang quá khứ huy hoàng, hoạt động khoa học nghiên cứu ở Âu châu - quê hương của lượng tử và tương đối, hai trụ cột của vật lư hiện đại mà hơn ai hết Max Planck và Albert Einstein đóng góp vào - đă phần nào bị lu mờ trong nửa thế kỷ sau Đệ nhị Đại Thế chiến 1939-1945 thảm khốc và phân hoá Đông - Tây. Năm nay 2008 mở đầu một bước ngoặt đánh dấu sự phục hưng của nền vật lư ở châu lục này với hai sự kiện nổi bật: trên trời có vệ tinh Planck được phóng lên không trung với kính viễn vọng tân kỳ để quan sát đo lường ánh sáng tàn dư từ thuở Nổ lớn (Big Bang) xẩy ra cách đây khoảng 13.7 tỷ năm với chi tiết chưa từng đạt, duới sâu hơn trăm thước trong ḷng đất có máy gia tốc hạt LHC (Large Hadron Collider) ở CERN ^[1] với chu vi 27 cây số, khắp năm châu duy nhất chỉ có máy này đạt tới năng lượng cực cao làm đầu tầu trong công cuộc khám phá, đào sâu t́m hiểu, thống nhất các định luật cơ bản tận cùng của vạn vật. Tháng Chín năm 2008, máy gia tốc LHC sẽ khởi động và chương tŕnh khám phá ưu tiên là việc săn t́m hạt cơ bản Higgs ^[2] , hạt tạo ra khối lượng cho vật chất, đề tài mũi nhọn của vật lư hiện đại, ch́a khóa mở đường cho sự thống nhất hoà quyện lượng tử với tương đối rộng. Xin nhắc lại, khối lượng là cơ nguyên khởi đầu của không-thời gian, của vạn vật, của vũ trụ. Không có khối lượng tức năng lượng th́ chẳng c̣n ǵ hết. Nền tảng của mô h́nh chuẩn là sự hiện hữu thiết yếu của hạt Higgs vô hướng tràn ngập không gian để cung cấp khối lượng cho tất cả các hạt khác khi tương tác với nó. Lư thuyết và thực nghiệm, tay trong tay vươn t́m những bến bờ xa xăm sâu thẳm nhất của tri thức khoa học, tiếp nối khát vọng chung của con người xưa nay không ngừng t́m hiểu thiên nhiên và bản thể của các hiện tượng. Hơn bao giờ hết và càng ngày càng rơ nét là cách tiếp cận cách tân của hai thế giới liên thông mật thiết: vĩ mô của vũ trụ bao la diễn giải bởi thuyết tương đối rộng và vi mô của hạt cơ bản diễn giải bởi thuyết lượng tử. Vệ tinh Planck và máy gia tốc hạt LHC theo thứ tự là hai công cụ thực nghiệm hiện đại sẽ khởi động năm nay 2008 trong công cuộc đo lường, t́m hiểu, khám phá, giải thích một cách nhất quán những bí ẩn của hai thế giới vĩ mô và vi mô nói trên. Ngành khoa học thống nhất và bổ túc lẫn nhau của hai thế giới đó mang tên gọi thiên văn-vật lư hạt (astro-particle physics). Xa xưa thiên văn ngụ ư ngắm nh́n quan sát thụ động các tinh tú vận chuyển, thêm bước nữa là thiên văn-vật lư t́m hiểu các hiện tượng phóng xạ và h́nh thành biến đổi của các thiên hà, tinh thể qua các định luật phổ quát của vật lư, ngày nay thiên văn hầu như đồng nghĩa với vũ trụ học và gốc nguồn của nó (tinh nguyên học) mà cốt tủy là thuyết tương đối rộng. Thuyết này như nàng Bạch Tuyết sau hơn nửa thế kỷ thiu thiu ngủ đă bừng tỉnh cùng ông hoàng lượng tử cất cánh vươn xa t́m biên giới của tri thức.

5a. Mấy bước ban đầu: Einstein là người trước tiên nhận ra cái toàn bộ chẳng sao tách biệt giữa vật chất-lực (cái bị chứa) và không-thời gian (cái vỏ chứa). Tất cả chỉ là một mà ông gọi là vũ trụ và khoa học nghiên cứu cái toàn bộ đó mang tên là vũ trụ học mà nguyên tắc - được ông xây dựng trong một công tŕnh ra đời tháng Hai năm 1917 - vẫn tiếp tục làm nền tảng rọi sáng cho măi đến ngày nay, mặc dầu thay đổi nhiều về chi tiết và mô h́nh ban đầu. Trước hết ông nhận thấy phương tŕnh (II) của thuyết tương đối rộng không có nghiệm số nào tương ứng với một vũ trụ vĩnh cửu bất biến với thời gian mà định kiến ngàn xưa đều tin chắc như vậy, ngay cả với con người cấp tiến như Einstein! Ông đành thêm vào vế trái phương tŕnh (II) một số hạng Λ gμν (ông gọi Λ > 0 là hằng số vũ trụ v́ nó chẳng có hệ quả cục bộ nào ở bất kỳ các quy mô lớn hay nhỏ) để có được một nghiệm số diễn tả vũ trụ ấm êm tĩnh lặng, tuy cong về không gian nhưng lại phẳng (không thay đổi) với thời gian. Nhưng chỉ vài năm sau đó, các nhà thiên văn vật lư W. de Sitter (Hà Lan), A. Friedmann (Nga) và G. Lemaître (Bỉ) khi xem xét toàn diện mười thành phần của phương tŕnh (II) chứng minh là vũ trụ không những cong về không gian mà cũng phải cong cả với thời gian, vậy vũ trụ hoặc dăn nở hoặc co nén chứ không tĩnh tại. Hỗ trợ quyết định cho phần lư thuyết trên là năm 1929 khi nhà thiên văn Mỹ E. Hubble đo lường quang phổ ánh sáng của các thiên hà và phát hiện chúng đồng loạt có tần số sóng bị giảm đi so với quang phổ đo trên trái đất. Tương tự như hiệu ứng Doppler trong âm thanh, theo đó tiếng sáo phát ra trên tàu chạy xa bến th́ người đứng yên trên bến nghe sáo trầm hơn, ngược lại nếu tàu tiến gần vào bến, tiếng sáo nghe bổng hơn ^[3] . V́ quan sát thấy tần số ánh sáng giảm, Hubble suy ra là khoảng cách từ chúng ta tới các thiên hà tỷ lệ thuận với tốc độ của chúng, càng ở xa vận tốc càng lớn. Như vậy vũ trụ không c̣n tĩnh lặng mà dăn nở như quả bóng khi ta bơm hơi vào, một thực tại chẳng sao chối căi. Sự kiện thiên văn quan trọng hàng đầu này ngày nay được xác định rất vững vàng bởi nhiều đo lường khác, do đó hằng số Λ (mà Einstein đưa ra như một tiên đề để giữ tĩnh lặng cho vũ trụ) chẳng c̣n cần thiết nữa khiến ông coi đó là sai lầm lớn nhất trong đời ḿnh. Nhưng cái ǵ làm vũ trụ dăn nở? Nhiều nhà vật lư cho rằng có thể chính là hằng số Λ, ai ngờ cái sai lầm hơn nửa thế kỷ trước, nay có thể trở nên một thành viên chủ yếu chiếm ngự đến 70 % năng lượng của hoàn vũ dưới cái tên mới là năng lượng tối để làm dăn nở vũ trụ, cái năng lượng tối đầy bí ẩn này chưa ai biết là ǵ tuy nhiên nó chẳng phải do vật chất tạo thành mà lại mang đặc tính năng lượng của chân không ^[4] . Việc tiên đoán sự dăn nở của vũ trụ thực là một kỳ công của thuyết tương đối rộng.

5b. Vụ Nổ lớn (Big Bang): Đo lường được vận tốc dăn nở (hằng số Hubble) của vũ trụ ngày nay, bạn hăy mường tượng thời gian lần ngược trở lại tựa như một cuốn phim chiếu giật lùi và thấy các thiên hà càng xa xưa bao nhiêu lại càng sát gần nhau bấy nhiêu khiến cho vũ trụ trước kia nhỏ hơn và phải có lúc xuất phát từ một khoảng không gian li ti. Ta suy ra khoảng 13.7 tỷ năm trước có một hiện tượng kỳ dị theo đó, từ một nguồn năng lượng và nhiệt độ vô hạn, nén ép trong một không gian cực kỳ nhỏ bé đă xẩy ra vụ Nổ lớn làm không gian dăn nở rồi lạnh dần để h́nh thành vũ trụ như ta quan sát ngày nay với hàng trăm tỷ thiên hà trong đó có giải sông Ngân và trái đất xanh lơ của chúng ḿnh. Nơi xảy ra vụ nổ lớn chính là chỗ bạn đang ở, cũng như ở bất cứ nơi đâu trong vũ trụ bao la v́ ở thời-điểm ấy, mọi chỗ ngày nay tách biệt hàng tỷ năm ánh sáng thực ra đă cùng chụm lại ở cái không-điểm kỳ dị ấy ^[5] , chẳng có một trung tâm vũ trụ ban đầu nào cả. Theo G. Gamow, phương pháp tinh tế nhất để kiểm chứng bằng thực nghiệm mô h́nh Big Bang là quan sát được hiện tượng bức xạ nền ^[6] , tức là sóng điện từ vi ba tràn ngập không gian. Đó là ánh sáng rơi rớt lại từ thuở Big Bang (nhiệt độ 1032 độ ban đầu cách đây khoảng 13.7 tỷ năm, nay nguội dần chỉ c̣n 2.735 độ K tuyệt đối). Bức xạ nền có hệ quang phổ của một vật đen ^[7] , đối tượng nghiên cứu đă đưa Planck đến giả thuyết lượng tử ^[8] . Mười năm qua chứng kiến nhiều phát triển trong sự hiểu biết của chúng ta về mô h́nh chuẩn vũ trụ mang tên gọi ΛCDM ^[9] mà ṇng cốt là vụ Nổ lớn.

5c. Lỗ đen: Ở nơi đâu tập trung mật độ năng-khối lượng càng lớn th́ sự biến dạng đàn hồi của không-thời gian càng nhiều ở đó, sự biến dạng tăng trưởng cho đến khi tính dẻo dai của nó bị đứt, tựa như cao su nếu bị kéo quá căng sẽ hết co dăn đàn hồi. Khi trọng trường lớn vô hạn, sự thay đổi trạng thái từ dẻo dai sang đứt vỡ làm xuất hiện các không-thời điểm kỳ dị, một hiện tượng tổng quát của thuyết tương đối rộng. Đại lượng đo sự biến dạng của không-thời gian là h00(x) ≈ hii (x) ≈ 2GM/(c2x), phụ chú 27. Khi 2GM/(c2x) ≈ 10–6 như trường hợp mặt trời, ta có thể dùng phép tính toán xấp xỉ gần đúng như Einstein đă dùng để giải đáp hiện tượng tuế sai của Thủy tinh và tiên đoán độ cong của ánh sáng khi đi gần mặt trời (phụ chú 32). Nhưng khi trọng trường cực mạnh như trường hợp lỗ đen và sao neutron, ta không thể dùng phép tính gần đúng nói trên nữa mà phải xét toàn diện chính xác phương tŕnh phi tuyến tính của Einstein. Sao neutron (ở đó electron và proton nén ép thành neutron và neutrino) có mật độ khối lượng vô cùng lớn, đường kính sao R chừng 10 km mà khối lượng M lại lớn như mặt trời, 2GM/(c2R) ≈ 0.4 (con số này so với 10–9 của trái đất), không gian trên sao neutron cong đến nỗi tổng cộng ba góc h́nh tam giác bằng 250 độ, nhịp độ tích tắc đồng hồ chậm bằng 78% so với đồng hồ chúng ta trên trái đất. Xin nhắc lại mô h́nh diễn tả cuộc đời của các thiên thể là tiến tŕnh tổng hợp nhiệt hạch của chúng, nôm na là sự phân ră tiêu thụ nhiên liệu hạt nhân nguyên tử của chúng. Quá tŕnh đó đưa đến cấu trúc nhiều vỏ bao quanh nhau của thiên thể, giống như củ hành với nhiều màng lớp. Nếu khối lượng của v́ sao đủ lớn, tác động của trọng trường khá mạnh làm tâm lơi của nó bị nén ép xô vào nhau và thu nhỏ lại, c̣n vỏ ngoài th́ bùng nổ tung bay và xuất hiện siêu sao mới (supernova) bừng sáng trong khoảnh khắc. Tùy theo khối lượng lớn bao nhiêu ban đầu, thiên thể này vào cuối đời (khi hạt nhân nguyên tử của nó bị phân ră hết) sẽ biến thành hoặc sao neutron hoặc lỗ đen, diễn tả trạng thái thiên thể bị co ép lại trong một không gian cực nhỏ. Lỗ đen là kết quả của sự sập đổ liên tục của một thiên thể có khối lượng lớn tới hạn, sự sập đổ đó không dừng lại khi h́nh thành sao neutron mà tiếp tục tới cùng để xuất hiện một không-thời gian kỳ dị (chân trời lỗ đen, 2GM/(c2R) = 1) ở đó từ vật chất đến ánh sáng và tín hiệu thông tin chẳng cái ǵ thoát ra khỏi ^[10] . Ngoài mật độ khối lượng M vô cùng lớn, lỗ đen c̣n mang điện tích Q và tự quay tṛn quanh trục của ḿnh với momen J, ba thông số (M,Q, J) xác định tính chất vật lư của nó. Khi nối kết với vật lư lượng tử, S. Hawking và J.D. Bekenstein khám phá ra là lỗ đen cũng phóng xạ nhiệt ra ngoài chân trời tối kín của nó như một vật đen và mang entropi luôn tăng trưởng, một liên hệ sâu sắc giữa vật lư cổ điển (trọng trường, nhiệt động học) và lượng tử.

5d. Đâu rồi phản vật chất? Sự hiện hữu của phản vật chất (do Paul A.M. Dirac dùng suy luận mà tiên đoán và C. Anderson khám phá ra sau đó) là hệ quả sâu sắc nhất của bản giao hưởng tuyệt vời giữa hai cột trụ của vật lư hiện đại: tương đối hẹp và lượng tử ^[11] . Máy chụp h́nh nổi PET (Positron Emission Tomography) trong y học ngày nay là một ứng dụng trực tiếp của hạt phản electron hay positron để rọi sáng chi tiết vi mô trong năo bộ. Có vật chất th́ cũng phải có phản vật chất, khi tụ hội chúng tự hủy để biến thành năng lượng, và ngược lại nếu đủ năng lượng th́ các cặp vật chất-phản vật chất được tạo ra và đó là chuyện thường xuyên xẩy ra trong các máy gia tốc hạt. Vũ trụ lúc nổ lớn chỉ chứa đựng duy nhất năng lượng với nhiệt độ vô cùng cao, từ đó khi nguội dần nẩy sinh ra vật chất và phản vật chất, chúng tương tác, biến chuyển, phân ră tuân theo bốn định luật tương tác cơ bản của vật lư: mạnh, yếu, điện từ, hấp dẫn. Số lượng vật chất và phản vật chất phải bằng nhau chẳng cái nào nhiều hơn cái nào v́ chúng đều khởi sinh vài phút sau Big Bang từ năng lượng thuần khiết ban đầu. Bức xạ nền - mà COBE, WMAP và sau hết vệ tinh Planck năm nay sẽ khởi động đo lường với chi tiết chưa từng đạt - chẳng bảo cho ta ánh sáng tàn dư đó chính là sản phẩm của sự va chạm cách đây 13.7 tỷ năm giữa vật chất và phản vật chất nẩy sinh từ năng lượng cực lớn sao? Mà vật chất chính là nguyên tử, khí và thiên thể giăng đầy vũ trụ ngày nay, c̣n phản vật chất lại chẳng thấy tăm hơi, tại sao vũ trụ ngày nay lại chỉ có vật chất? Đó là một bí ẩn của mô h́nh Big Bang v́ ba lực (mạnh, điện từ và hấp dẫn) trong bốn tương tác nói ở trên đều tuân theo luật đối xứng vật chất-phản vật chất (đối xứng CP, nói theo ngôn từ của lư thuyết chuẩn các hạt cơ bản), không có sự dị biệt giữa chúng. Chỉ tương tác yếu (ba thí dụ điển h́nh của tương tác này: sự tổng hợp nhiệt hạch trong tâm mặt trời và các tinh tú, sự phân ră β của các hạt nhân nguyên tử và hạt neutrino) mới vi phạm phép đối xứng CP, theo đó tương tác yếu của phản vật chất và của vật chất không giống y hệt nhau mà khác đôi chút. Sự khác biệt đó được diễn giải hoàn hảo trong mô h́nh chuẩn hạt cơ bản và được kiểm chứng vô cùng chính xác bằng thực nghiệm. Nhưng sự vi phạm nhỏ của phép đối xứng vật chất-phản vật chất trong các pḥng thí nghiệm trên trái đất không giải thích nổi về mặt định lượng tại sao trong vũ trụ ngày nay vật chất lại áp đảo toàn diện phản vật chất, tại sao cái này lại biến đi ngay từ trong trứng nước thời Nổ lớn? Trong việc diễn giải sự vi phạm đối xứng vật chất-phản vật chất, tại sao mô h́nh chuẩn hạt cơ bản thành công mà mô h́nh chuẩn vũ trụ Big Bang lại thất bại? Đó là đề tài nghiên cứu ưu tiên của LHC cùng với sự săn t́m hạt cơ bản Higgs (phụ chú 34).

5e. Sóng trọng trường: Nếu điện thoại và máy vi tính di động tân kỳ là tảng băng nổi của sóng điện từ trường với bốn phương tŕnh Maxwell ^[12] mà công nghệ thông-truyền tin hiện đại khai thác tuyệt vời, th́ sự hiện hữu của sóng trọng trường là hệ quả tất yếu của mười phương tŕnh Einstein trong thuyết tương đối rộng, minh họa tính dẻo đàn hồi của không-thời gian. Tiến tŕnh khai thác và ứng dụng của sóng trọng trường là cả một chân trời kỳ diệu đang hé mở. Thời cổ điển truớc Einsein mọi người mặc nhiên chấp nhận khái niệm tiên nghiệm của không-thời gian cứng nhắc chẳng chút nào liên đới đến vật chất-năng lượng chứa đựng ở trong. Einstein qua thuyết tương đối rộng chỉ dẫn cho ta một nhận thức khác hẳn: sự phân phối năng-khối lượng vật chất (thí dụ hệ thống hai lỗ đen dao động và hút nhau) không những bẻ cong cấu trúc không-thời gian mà sự biến dạng đó lại truyền đi vô tận khắp nơi dưới dạng sóng với vận tốc c của ánh sáng. Vậy sóng trọng trường phản ánh sự phân phối dao động của vật chất và sự biến dạng đàn hồi của không-thời gian, một đặc trưng của thuyết tương đối rộng. Tín hiệu để nhận diện và đo lường được sóng trọng trường là sự thay đổi δL của khoảng cách L giữa hai vật bị nhiễu loạn bởi sóng đi qua nó, cái thay đổi δL/ L đó quá nhỏ khoảng 10–22 mà các giao thoa kế như Ligo (Mỹ), Virgo và Geo (Âu châu), Tama (Nhật) cùng Lisa (quốc tế) đang và sẽ tích cực đo lường.

5f. Chân không lượng tử và sự dăn nở vũ trụ với hằng số Λ: Chân không lượng tử (quantum vacuum), viết gọn thành Không được định nghĩa như trạng thái cơ bản tận cùng của vạn vật, nó vô hướng, trung ḥa, mang năng lượng cực tiểu trong đó vật chất, tức là tất cả các trường lượng tử kể cả điện từ, đều bị loại bỏ hết. Nhưng không phải v́ Không chẳng chứa trường vật chất nào mà năng lượng của nó bằng 0. Theo nguyên lư bất định Heisenberg, năng lượng của bất cứ trạng thái vi mô nào là chuỗi (1/2)hν, (3/2)hν, (5/2) hν...chứ không phải là 0hν, 1hν, 2hν... Cũng dễ hiểu thôi, nguyên lư bất định bảo ta nếu xung lượng |k| được xác định rơ rệt bao nhiêu th́ vị trí trong không gian |x| lại mơ hồ rối loạn bấy nhiêu, vậy năng lượng tối thiểu ε = (1/2) hν ≠ 0 chính là một thỏa hiệp tối ưu b́nh đẳng cho cả hai bên |k| và |x|. Thực thế, nếu ε  = 0, |k| = 0, vậy |x| không sao được xác định nổi. Phản ánh nguyên lư này, thế giới vi mô luôn luôn dao động ngay ở nhiệt độ tuyệt đối thấp nhất (năng lượng cực tiểu) và đó là ư nghĩa của sự thăng giáng lượng tử (quantum fluctuation). Thang mức vi mô nói chung là cả một vũ đài náo nhiệt và hỗn loạn, "vạn vật sinh hủy, hủy sinh, ôi phí phạm thời gian" như nhà vật lư kỳ tài Feynman từng hài hước. Không gian trống rỗng tưởng như yên tĩnh phẳng lặng thực ra chỉ là tổng quan trung b́nh của một thực tại vô cùng phong phú và sôi sục ở mực độ sâu thẳm, tựa như biển hiền ḥa nh́n phiến diện trên bề mặt phẳng mượt vậy mà đang diễn ra dưới ḷng sâu một đợt sóng ngầm dao động liên hồi. Bởi năng lượng cực tiểu khác 0 và v́ tần số ν có thể là bất cứ con số nào từ 0 đến vô tận nên Không có năng lượng phân kỳ ^[13] khi ta lấy tích phân tất cả các mốt dao động. Tuy chẳng sao định lượng nổi (v́ năng lượng phân kỳ), nhưng chân không lượng tử vẫn có thể biểu hiện tác động của nó qua hiệu ứng Casimir ^[14] , một đặc trưng quan sát đo lường được. Chính v́ vô hướng, trung ḥa lại có năng lượng vô hạn, nên chân không lượng tử mang ẩn dụ một hư vô mênh mang tĩnh lặng, từ đó do những kích thích nhiễu loạn của năng lượng trong Không mà vật chất (cùng phản vật chất) được tạo thành để rồi chúng tương tác, biến đổi, phân ră rồi trở về với Không, cứ thế tiếp nối bao ṿng sinh hủy! Chân không lượng tử chính là trạng thái cơ bản, cội nguồn và chốn trở về cũng như ra đi của vạn vật. Nó không rỗng tuếch chẳng có ǵ mà là cái thế lắng đọng của tất cả. Chân không-Vật chất-Không gian-Thời gian chẳng sao tách biệt, đó là hệ quả của Tương đối (hẹp và rộng) hợp phối cùng Lượng tử! Nhưng năng lượng cực kỳ lớn của chân không lượng tử (tai họa chân không) lại vượt xa quá nhiều mật độ năng lượng tối làm dăn nở vũ trụ mà các nhà thiên văn ước lượng bằng cách đo lường gia tốc của các siêu sao mới. Xin nhắc lại năng lượng tối mang đặc tính của chân không (với hằng số Λ vô hướng, xem 5(a) và các phụ chú 36, 41). Điều này minh họa sự mâu thuẫn cơ bản giữa hai trụ cột của vật lư hiện đại lượng tử và tương đối rộng.


6. Tạm kết

Hai thuyết lượng tử và tương đối rộng đều cần thiết để diễn tả các hiện tượng vật lư khi hai thế giới vi mô và vĩ mô cận kề chẳng c̣n tách biệt như trong trung tâm sâu thẳm của lỗ đen, trong trạng thái vũ trụ ở kỷ nguyên Planck (giây phút ban đầu của Big Bang với nhiệt độ kinh hoàng, không gian độ dài Lp cực nhỏ, năng lượng Ep cực lớn, phụ chú 45), hoặc trong các máy gia tốc hạt năng lượng cao mà LHC là điển h́nh tốt đẹp nhất. Ở những điều kiện cực độ ấy, các định luật của trọng trường và của lượng tử không tương thích với nhau, h́nh học không-thời gian cong uốn trơn tru của thuyết tương đối rộng lại xung đột sâu sắc nhất với cái sôi động, thăng giáng lượng tử, các phương tŕnh của hai thuyết khi kết hợp cho ra những đáp số vô hạn, phi lư. Ngoài ra ở kỷ nguyên Planck, cường độ của trọng lực (không đáng kể ở nhiệt độ và năng lượng b́nh thường) không c̣n nhỏ nữa mà tương đương với cường độ của ba lực cơ bản khác: điện-từ, mạnh và yếu. Ba lực này thành công tuyệt vời trong sự ḥa đồng với cơ học lượng tử và như vậy chúng diễn tả chính xác và nhất quán mọi vận hành từ thế giới vi mô hạ nguyên tử đến thế giới vĩ mô của các thiên thể trong vũ trụ bao la. Theo thứ tự, sự phối hợp với lượng tử của ba lực cơ bản trên mang tên điện động lực học lượng tử (QED, Quantum Electro-Dynamics), Sắc động lực học lượng tử (QCD, Quantum Chromo-Dynamics) và Điện-Yếu lượng tử (Quantum Electro-Weak Interaction), tóm tắt trong Mô h́nh chuẩn hạt cơ bản với không dưới hai chục giải Nobel trong khoảng 30 năm gần đây. Có thể khẳng định rằng điện động lực học lượng tử là nền tảng phát triển kỳ diệu của công kỹ nghệ thông-truyền tin hiện đại với vi điện tử, quang điện tử, spin-điện tử.

Trong khi đó, luật hấp dẫn lại mâu thuẫn với lượng tử. Nguyên nhân sự khác biệt giữa ba lực trên với trọng lực - khi cả bốn kết hợp với nguyên lư bất định Heisenberg (bị lượng tử hoá, nói theo ngôn từ chuyên môn) - có thể nhận ra như sau: các trường (vật chất và điện từ) của ba lực khi bị lượng tử hóa sẽ biến thành đơn vị rời rạc vận hành trong một không-thời gian liên tục trơn tru. Trái lại trọng trường theo thuyết tương đối rộng lại chính là metric của không-thời gian trơn tru liên tục đó, khi bị lượng tử hóa cái trơn tru ấy chẳng c̣n giữ lại được đặc tính dẻo dai nguyên thủy nữa mà bị mất tính đàn hồi, có nếp gấp và lỗ thủng (nói theo ngôn ngữ toán học topo) tựa như mảng cao su căng quá bị xé rách. Ta không thể không cảm thấy có cái ǵ trục trặc ở mức cơ bản nhất, tại sao thiên nhiên lại có thể tùy tiện phân chia những định luật, chính xác ở một quy mô nào đó, để rồi trở thành vô lư ở thang mức khác, cái nghịch cảnh này chỉ phản ảnh sự thiếu sót của ta trên đường t́m kiếm luật hấp dẫn lượng tử (Quantum Gravitation). Đó quả là vấn đề số một của vật lư hiện đại mà tai họa chân không minh họa ở trên là thí dụ.

Thuyết siêu dây (Superstring) là một trong vài ^[15] lư thuyết mang khả năng, về nguyên tắc, dung ḥa và giải quyết mâu thuẫn nói trên để mô tả nhất quán tất cả bốn tương tác cơ bản trong cả hai thế giới cực lớn của vũ trụ bao la và cực nhỏ của hạ nguyên tử, thống nhất mọi điều về một mối. Theo thuyết này, thành phần cấu trúc cơ bản của vạn vật không phải là hạt điểm (0 chiều) mà là dây hay màng (1 hay nhiều chiều) cực nhỏ với kích thước độ dài Planck cỡ 10–35 m luôn dao động. Hai nền tảng mà thuyết siêu dây dựa vào là tương đối hẹp và lượng tử, như vậy lúc khởi đầu có sự cách biệt giữa cái vỏ chứa (không-thời gian phẳng Minkowski) và cái bị chứa (dây đàn hồi dao động). Ngạc nhiên thay, kết quả điểm đến là cái bị chứa chuyển giao tính đàn hồi cho cái vỏ chứa, cái không-thời gian này hết cứng nhắc mà trở thành cong uốn đàn hồi của thuyết tương đối rộng, như vậy trọng lực là hệ quả tất yếu suy ra từ siêu dây. Một đặc điểm khác, siêu dây là thuyết duy nhất đầu tiên trong vật lư xác định được con số D = 10 chiều của không-thời gian (trước siêu dây, số chiều 4 của không-thời gian ta quen dùng chỉ là một định đề tiên nghiệm ta tự cho ta, do cảm nhận và quan sát) minh họa không-thời gian là bộ phận chẳng thể tách rời khỏi vật chất mà thuyết tương đối rộng đă hé mở cho ta thấy. Sáu chiều không gian c̣n lại, tuy bị cuốn tṛn quá nhỏ để ta không quan sát được trong đời sống hàng ngày, có thể làm thay đổi chút xíu luật 1/R2 của trọng lực Newton, một đề tài thực nghiệm nóng hổi. Đặc điểm thứ ba của siêu dây là khả năng thống nhất điện từ với trọng lực mà Einstein trăn trở t́m kiếm không thành, nôm na điện-từ trường như siêu dây hở (hai đầu dây tự do) và trọng trường như siêu dây kín (ṿng kín). Nhưng cần nhấn mạnh là mặc dầu có những tiến bộ kinh ngạc, nhiều khía cạnh lư thuyết của siêu dây c̣n xa mới hoàn toàn sáng tỏ và nhất là không có một tiên đoán nào của nó được chứng nghiệm dẫu gián tiếp. Edward Witten - chuyên gia đầu ngành của thuyết này, nhà vật lư đầu tiên được huy chương Fields uy tín về toán, không một nhà vật lư nào, kể cả những giải Nobel, có công tŕnh được trích dẫn nhiều bằng ông - đă một lần tuyên bố: thuyết siêu dây là một bộ phận của vật lư thế kỷ 21 đă t́nh cờ rơi xuống thế kỷ 20, ngụ ư có lẽ cần biết bao năm nữa mới được hoàn tất! Cơ sở toán học của nó quá phức tạp, các chuyên gia siêu dây phải tự ḿnh ṃ mẫm sáng tạo, không như Einstein đă sẵn có h́nh học cong Riemann làm nền để khai sinh ra thuyết tương đối rộng.

Vào cuối thế kỷ thứ 19, có một mâu thuẫn giữa một bên là lư thuyết điện từ + nhiệt động học - hai trụ cột cơ bản của vật lư thời đó - và bên kia là thực nghiệm đo lường về hiện tượng bức xạ nhiệt của vật đen. Thực thế, lư thuyết trên đưa đến một hệ quả phi lư là tổng năng lượng phóng xạ bởi vật đen phải vô hạn, cụ thể ngồi trước một bếp sưởi hồng, bất kỳ nhiệt độ cao thấp ra sao ta sẽ bị thiêu cháy tan biến hết! Vậy mà Lord Kelvin, người của nhiệt độ tuyệt đối, giáo hoàng của vật lư thời đó có câu tuyên bố năm 1892 nổi tiếng v́ lạc quan: “Vật lư đă hoàn chỉnh cả rồi về mặt căn bản, cái mà ta c̣n có thể đóng góp chỉ là xác định thêm vài thập phân sau dấu phẩy cho các đo lường, tính toán mà thôi. Tuy nhiên hăy c̣n hai vấn đề nho nhỏ...”. Hai tiểu tiết ông nêu lên là: thứ nhất Michelson và Morley chẳng t́m thấy chất liệu ether (xem 3a và phụ chú 12) tràn ngập vũ trụ trong đó dao động sóng điện từ, thứ hai các đo lường ngày càng chính xác về cường độ bức xạ nhiệt của vật đen (phụ chú 39) không phù hợp với nền tảng căn bản của vật lư kèm thêm cái hệ quả phi lư nói trên. Ngờ đâu đó chính là hai vấn đề cốt lơi làm ngọn hải đăng chỉ đường cho khoa học vượt trùng dương đi t́m biên giới của tri thức. Giải quyết được hai tiểu tiết trên theo thứ tự là Albert Einstein với thuyết tương đối hẹp, và Max Planck với thuyết lượng tử ^[16] , hai trụ cột của vật lư hiện đại. Ai có thể tưởng tượng nổi trăm năm sau ư tưởng của Planck, một phần ba tổng sản lượng kinh tế của cường quốc số một thế giới hiện nay có gốc nguồn từ những ứng dụng trực tiếp của công nghệ lượng tử. Cái kiêu hănh vội vàng của Lord Kelvin cho ta bài học nhún nhường về hiểu biết hạn hẹp cục bộ của con người so với cái không biết mênh mông. Qua con mắt ngây thơ của các em trẻ hỏi ta đủ thứ, cái khát vọng hướng thượng, t́m hiểu, học hỏi, sáng tạo có lẽ chính là đặc tính bẩm sinh của loài người. Như chim di đứng trên đôi cánh của chim bằng để cùng nh́n cao xa hơn mà Besso thuở nào nói về bạn Einstein, dựa trên thành quả của người đi trước, mỗi chúng ta từ trái đất nhỏ nhắn cùng nhau góp phần cho sự hài ḥa giữa người với người và với môi trường thiên nhiên để vươn tới các v́ tinh tú trong hoàn vũ bao la.

© 2008 talawas

^[1]Quả là một bài học vượt xa đối tượng khoa học thuần tuư. Trên cánh đồng hoang ở biên giới Pháp-Thụy Sĩ gần thành phố Genève, ngay sau Đệ nhị Thế chiến nhiều nhà vật lư Âu châu di tản khắp nơi v́ nạn phát xít đă trở về cố hương cùng đồng nghiệp ở lại xây dựng nên Trung tâm Âu châu Nghiên cứu Hạt nhân (CERN). V́ ḥa b́nh và phát triển qua nghiên cứu cơ bản, với sự hỗ trợ tích cực của một số chính khách có tầm nh́n xa, họ đă chung sức mở đường cho sự hồi sinh và hoà giải của các nước Âu châu, đặc biệt Đức-Pháp. V́ mỗi nước riêng lẻ không sao đủ nhân sự và phương tiện để hoàn thành sứ mạng, nguyên tắc tổ chức của CERN (tập hợp đóng góp tài năng ngân quỹ từ nhiều nước châu Âu, chủ yếu từ Đức, Pháp, Anh, Ư) đă tiên phong làm mô h́nh cho nhiều ngành hoạt động khác phỏng theo như thiên văn, sinh học, thậm chí cả kinh tế, chính trị (CERN ra đời nhiều năm trước Liên hiệp Âu châu). Mạng lưới toàn cầu (world wide web) của internet ra đời ở CERN là một trong nhiều thành công kỳ diệu từ nghiên cứu cơ bản sang ứng dụng của cơ quan này, kỹ thuật siêu dẫn điện từ dùng trong máy gia tốc hạt khổng lồ LHC là một thí dụ khác. Năm 1992 (đúng 500 năm Columbus khám phá ra châu Mỹ) máy gia tốc hạt SCC đầu tầu thế giới về vật lư hạt cơ bản đang được xây ở Dallas, Texas (Mỹ) bị cắt đứt hỗ trợ. May thay CERN quyết tâm thay thế sự hẫng hụt này và trong mười năm xây dựng nên LHC (http://public.web.cern.ch/Public/Welcome.html) để mở đầu chu kỳ thăng trầm rời Mỹ sang Âu của ngành vật lư hạt mũi nhọn này.
^[2]Peter Higgs, tên nhà vật lư xứ Scotland đă đề xuất phải có hạt này để mang khối lượng cho vật chất. Tất cả các hạt cơ bản (trừ hạt cuối cùng Higgs) của mô h́nh chuẩn như quark, lepton, gluon, photon, W, Z đều đă được khám phá hết cả rồi với độ chính xác tuyệt vời. Các nhà vật lư ngóng chờ hạt Higgs với tất cả hồi hộp, nếu t́m thấy, mô h́nh chuẩn sẽ là hệ h́nh có tính quyết định cho sự hiểu biết tận tường gốc nguồn của khối lượng vật chất, và có tác động sâu xa đến vũ trụ học. Nếu không, ta sẽ đứng trước một bước ngoặt lịch sử của vật lư hạt cơ bản, nền tảng của mô h́nh chuẩn sẽ bị lung lay v́ thiếu nhất quán.
^[3]Các chuyên gia gọi tần số ánh sáng bị giảm đi là sự xê dịch về phía đỏ (red shift), hàm nghĩa ánh sáng màu đỏ có tần số nhỏ hơn ánh sáng màu xanh. Lư do là v́ nếu nguồn sáng hay âm thanh chuyển động ra xa (đến gần) bến, ánh sáng hay âm thanh sẽ mất nhiều (ít) thời gian hơn để tới người quan sát trên bến, bước sóng trên bến v́ đó sẽ dài (ngắn) đi, hay tần số sóng sẽ giảm (tăng).
^[4]Khi ta chuyển Λgμν từ vế trái sang vế phải của phương tŕnh Einstein (II), ta thấy tenxơ năng-xung lượng Tμν có thêm một số hạng mới δTμν = – (Λc4/8πG) gμν. Số hạng mới này mang đặc tính của một chân không (v́ Λ vô hướng và gμν có gốc nguồn thuần h́nh học, chẳng do năng-xung lượng của vật chất tạo nên), hơn nữa dấu trừ của δTμν có tác động đẩy ra (thay v́ hút vào bởi lực hấp dẫn +8πG/c4Tμν của vật chất làm không gian co lại). Vậy δTμν coi như tác động phản hấp dẫn của chân không làm dăn nở vũ trụ và năng lượng tối chỉ định tính chất này.
^[5]Một số sách báo phổ biến khoa học khi đề cập đến Big Bang thường dùng ngôn từ gợi ư có ḍng thời gian trôi chảy từ quá khứ đến tương lai mà cả hai thuyết tương đối hẹp và rộng đều phủ định. Big Bang không phải là sự khai sinh ra vũ trụ từ hư vô, nó là một khoảnh mép không-thời gian bị biến dạng rất mạnh bởi năng-xung lượng cực kỳ lớn, do đó trạng thái đàn hồi của không-thời gian bị đứt tựa như miếng cao su quá căng mà bị xé rách.
^[6]A. Penzias và R. Wilson năm 1965 đă t́nh cờ gián tiếp phát hiện ra bức xạ nền của vũ trụ (CMB, Cosmic Microwave Background), rồi năm 1992 G. Smoot và J. Mather dùng vệ tinh COBE chụp ảnh trực tiếp đấu tiên, mới đây 2003 là vệ tinh WMAP với chi tiết tinh vi hơn và năm nay 2008 vệ tinh Planck hy vọng chứng nghiệm được thời lạm phát tức là khoảng 10–35 giây sau Big Bang.
^[7]Đúng là các nhà vật lư ít người có cái duyên thi sĩ nên chỉ thấy toàn những tên vật đen, lỗ đen, nổ lớn, vật chất tối, dây! Trong đời sống hàng ngày, ta gọi vật đen (black body) là một chất liệu chỉ hấp thụ ánh sáng chiếu lên nó mà không phản xạ nhưng vẫn phóng xạ. Trong pḥng thí nghiệm, vật đen là một ḷ bịt kín nung nóng ở nhiệt độ T và đục một lỗ nhỏ trên thành ḷ, ta nghiên cứu bức xạ nhiệt phát ra qua lỗ. Sự phân phối cường độ bức xạ phát ra bởi vật đen chỉ phụ thuộc vào T thôi chứ không vào bất cứ chất liệu nào ở trong ḷ. Điều này chứng tỏ bức xạ của vật đen chỉ phụ thuộc vào sự dao động của các thành phần cơ bản chung cho tất cả các chất liệu, mang tính chất rất phổ quát. Bức xạ nhiệt của vật đen là một trường hợp hi hữu trong vật lư có tính phổ quát. Vật đen lư tưởng là hoàn vũ sau vụ Nổ lớn mà hai vệ tinh COBE và WMAP (sắp tới là vệ tinh Planck) đo lường tàn dư của nhiệt lượng phóng xạ cách đây khoảng 13.7 tỷ năm mà giải Nobel vật lư 2006 trọng thưởng.
^[8]Bằng một “hành động hầu như tuyệt vọng” để giải đáp cường độ và nghịch lư (năng lượng vô hạn) của vật đen, Planck đưa ra một giả thuyết theo đó các vật thể khi dao động với tần số ν th́ năng lượng E phát ra phải theo từng ‘gói‘ rời rạc như 1hν, 2hν, 3hν... chứ không liên tục. Kỳ lạ thay năng lượng phun ra từng gói từng chùm chứ không tuôn chảy đều đặn. Einstein là người đầu tiên dùng giả thuyết này để diễn giảng hiện tượng quang điện, mở đầu cho sự khám phá ra lưỡng tính vừa sóng vừa hạt của ánh sáng cũng như của các vật thể vi mô khác (như electron) và sự ra đời của vật lư lượng tử với nguyên lư bất định Heisenberg. Hằng số Planck h (trong phương tŕnh E = hν) có gốc nguồn ở chữ Hilfe (tiếng Đức nghĩa là phụ trợ), chi tiết này nói lên cái khiêm tốn của một nhà bác học lớn, dẫu trong thâm tâm Planck biết ḿnh vừa hé mở một chân trời mới khi thổ lộ với con trai Erwin 7 tuổi: hôm nay bố phát minh ra một điều phi thường chẳng kém Newton.
^[9]Λ chỉ định hằng số vũ trụ Λ gắn liền với năng lượng tối, c̣n CDM viết tắt của Cold Dark Matter. Vật chất tối (dark matter), chiếm tới 27% tổng khối lượng vật chất trong vũ trụ, là vật chất không bức xạ mà chỉ có vai tṛ tác động lên cách vận hành của các thiên hà, nó khác lạ với vật chất b́nh thường (chỉ chiếm khoảng 3% khối lượng vũ trụ) của những thiên hà sáng ngời mà ta quan sát được. Gốc nguồn của giả thuyết vật chất tối đi từ sự đo lường vận tốc quay rất cao của các thiên hà, hệ quả của vận tốc quá cao này là các thiên thể phải tung bay khắp phía mà không gộp lại được thành cḥm như ta quan sát, do đó giả thuyết phải có vật chất tối để lôi hút các thiên hà sát lại gần nhau. Phần c̣n lại (khoảng 70% tổng năng-khối luợng trong vũ trụ) là năng lượng tối (dark energy) để làm vũ trụ dăn nở. Cần nhấn mạnh bản chất bí ẩn của năng lượng tối (mang tính chất đẩy ra) và của vật chất tối (mang tính chất hút vào), chúng là ǵ, một đề tài nóng hổi của vũ trụ học và vật lư hạt cơ bản.
^[10]H́nh học không-thời gian của một lỗ đen đơn giản nhất (diễn tả bởi khối lượng M) có dạng sau đây:
ds2 = – A c2 dt2 + dr2 /A + r2 (dθ2 +sin2θ dφ2 ) với A = 1 – (2GM /c2 r)
mà Schwarzschild t́m ra năm 1916.
Ta thấy metric g00 = – A sẽ bằng 0 nếu r = RH ≡ 2GM /c2 . Khi g00 = 0, theo phương tŕnh (3) của phụ chú 29, ánh sáng tần số ν0 phát ra từ bất kỳ điểm nào trên h́nh cầu RH bán kính RH th́ người ở ngoài h́nh cầu (r > RH) sẽ thấy ánh sáng ấy chỉ có một tần số ν duy nhất bằng 0 (v́ ν/ν0 lúc nào cũng = 0). Vậy h́nh cầu RH chính là chân trời lỗ đen v́ ánh sáng trong đó không phát hiện nổi ra cho người ở ngoài quan sát được.
^[11]Theo thuyết tương đối hẹp, vật chất khối lượng m chuyển động với xung-lượng k mang một năng lượng E, ba đại lượng đó liên kết bởi E2 = |k|2c2 + m2c4 và E2 = m2c4  chỉ là dạng riêng lẻ của phương tŕnh trên khi hạt có khối lượng m ≠ 0 không di động (|k|= 0). Công thức E2  = |k|2c2 + m2c4  của thuyết tương đối hẹp và chùm năng lượng hν của thuyết lượng tử là điểm khởi đầu mà Dirac kết hợp được để khám phá ra một chân trời mới: sự xuất hiện của phản hạt có cùng khối lượng với hạt, nhưng tất cả các đặc trưng khác (điện tích, spin, lượng tử tính) của hạt và phản hạt đều ngược dấu. Sự thống nhất cơ học lượng tử với thuyết tương đối hẹp là điều tối cần thiết v́ thế giới vi mô của lượng tử luôn dao động với vận tốc rất cao, mà trường hợp này chỉ thuyết tương đối hẹp của cơ học mới diễn tả được chính xác. Để chứng minh phản hạt, Dirac đi từ nhận xét sau đây: v́ E  = ± (|k|2c2 + m2c4 )½, nên E  = ± mc2 với một vật bất động. Trong vật lư cổ điển, E > 0 nên ta chỉ có E = mc2  thôi. Trái lại trong thế giới vi mô của vật lư lượng tử, năng lượng của một hạt có thể mất đi hay nhận được từng gói hν, vậy không có ǵ ngăn cản hạt khi mất đi quá nhiều gói hν có thể mang năng lượng âm, hay ngược lại một hạt  với E <  0 khi nhận được nhiều gói  hν có thể trở về trạng thái năng lượng dương. Thí dụ trong đại dương của muôn vàn hạt electron (điện tích âm -e ) mang E <  0, nếu ta có đủ sức để kéo một electron trong đại dương ấy ra ngoài, tức là đại dương ấy mất đi một electron mang  E < 0, -e. Nhưng mất đi (tượng trưng bằng dấu -) cái âm th́ cũng như nhận được cái dương, -(-) = +, vậy kết cục là ta thấy xuất hiện một hạt có điện tích dương +e và mang năng lượng E > 0. Đó là hạt phản electron hay positron. Tóm lại, hạt và phản hạt có E > 0, chúng có chung khối lượng nhưng mọi đặc trưng khác (điện tích, spin, lượng tử tính) đều ngược dấu.
^[12]Ludwig Boltzmann (1844-1906) - nhà vật lư và triết học uyên thâm Áo, người đặt nền tảng cho vật lư thống kê - khi suy ngẫm về bốn phương tŕnh điện-từ Maxwell viết dưới dạng (∂α ∂α)Aμ = Jμ đă thốt lên “Phải chăng Thượng đế viết những ḍng này!”, có lẽ ông c̣n kinh ngạc nữa nếu biết đến phương tŕnh Einstein và sóng trọng trường.
^[13]Làm sao ước tính được năng lượng của Không? Phép phân tích thứ nguyên cho ta cách trả lời. Với ba đại lượng cơ bản phổ cập trong vật lư là h = 2π ћ hằng số Planck, G hằng số trọng lực Newton và c vận tốc ánh sáng, ta chỉ có một cách duy nhất để lập nên những đại lượng mang thứ nguyên chiều dài (L), khối lượng (M), và thời gian (T). Đó là chiều dài Planck Lp = [Gћ /c3]½ = 1.6 × 10−35 m, khối lượng Planck Mp  =  ћ /(cLp) = 2.2 × 10−8 kg = 1.2 x 1019 GeV/c 2, và thời điểm Planck Tp = Lp /c  = 5.4 × 10−44 s. Từ đó, năng lượng Planck Ep  =  Mpc 2 = 2 × 10+9 joule. Mật độ năng lượng của Không được ước tính theo (27/16π2) Ep/(Lp)3 = 8.4 × 10112  joule/ m3 với những đóng góp của các trường ảo tràn đầy trong Không:  photon trong tương tác điện từ, ba boson W±, Z0 của tương tác yếu, và tám gluon trong tương tác mạnh. Đóng góp của các hạt cơ bản quark và lepton cũng chẳng thay đổi nhiều công thức trên.
^[14]Trong một hư không kín rỗng, không ánh sáng không chút vật chất, ta đặt hai phiến gương mỏng song song. Mặc dầu năng lượng giữa hai phiến và ngoài hai phiến của Không đều phân kỳ như ta biết, nhưng năng lượng của Không ở giữa nhỏ hơn ở ngoài hai phiến (v́ kích thước ở giữa nhỏ hơn ở ngoài), sự khác biệt hữu hạn đó gây nên một áp suất làm chúng hút lẫn nhau. Đó là lực Casimir, một đặc trưng của lượng tử. Lực hút đó ông tính được ra bằng Fc = (πhc/120) (L2/d 4) với L2  là diện tích của gương và d khoảng cách giữa hai phiến. Nguồn gốc lượng tử của Fc được biểu hiện rơ ràng qua h (hằng số Planck) trong công thức trên. Ở khoảng cách d ≈ nanô-mét (một phần tỷ mét) trong công nghệ tương lai, lực này có thể đóng vai tṛ quan trọng. Các pḥng thực nghiệm ở Riverside, Padova, Stockholm, Paris đă đo Fc với độ sai biệt nhỏ hơn 1% so với tính toán. Trong hư không tất cả đều vắng bóng chẳng có điện từ, ánh sáng, vật chất, khối lượng, điện tích, sắc tích...chi cả, kỳ lạ thay đột khởi một lực mà gốc nguồn rút tỉa từ năng lượng cực tiểu (nhưng vô hạn) của chân không lượng tử! Nhà vật lư Hà lan Hendrik Casimir, sau khi công bố năm 1948 lực mang tên ông, đă giữ chức vụ tổng giám đốc nghiên cứu đại tập đoàn công kỹ nghệ quốc tế Philips.
^[15]Một thuyết khác là h́nh học phi giao hoán (non-commutative geometry) do A. Connes (nhà toán học Pháp) đề xướng, theo đó không-thời gian cũng chẳng c̣n trơn tru liên tục nữa mà rời rạc thành đơn vị như vật chất.
^[16]Khởi động bởi Planck và tiếp nối bởi Einstein, vật lư lượng tử là một công tŕnh tập thể với những đóng góp của nhiều nhân vật lịch sử như Bohr, de Broglie, Schrödinger, Heisenberg, Dirac, Pauli, Fermi... nối tiếp cho măi đến ngày nay bởi các tài năng đến từ mọi miền trên trái đất qua vài khuôn mặt quen thuộc như Bose, Gell-Mann, Landau, Salam, Yang, Yukawa...